利用 Morris 遍历实现二叉树的先序,中序,后续遍历,时间复杂度 O(N),额外空间复杂度 O(1)。
1. 算法流程
Morrris 遍历利用叶子节点的左右空节点,达到 O(1) 的空间复杂度。
当前节点记为 cur(引用)。
- 如果
cur 没有左孩子(cur.left == null),将 cur 向右移动(cur = cur.right);
- 如果
cur 有左孩子 (cur.left != null),找到 cur 左子树上最右侧的节点,记为 mostRight:
- 如果
mostRight 的右孩子为空(mostRight.right == null),让其右孩子指向 cur(mostRight.right = cur),cur 向左移动(cur = cur.left);
- 如果
mostRight 的右孩子指向 cur(mostRight.right == cur),让其右孩子指向空(mostRight.right = null),cur 向右移动(cur = cur.right)。
2. 性质
将 Morris 遍历与普通的递归遍历进行对比:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
public void process(TreeNode root) {
if (root == null) {
return;
}
process(root.left);
process(root.right);
}
|
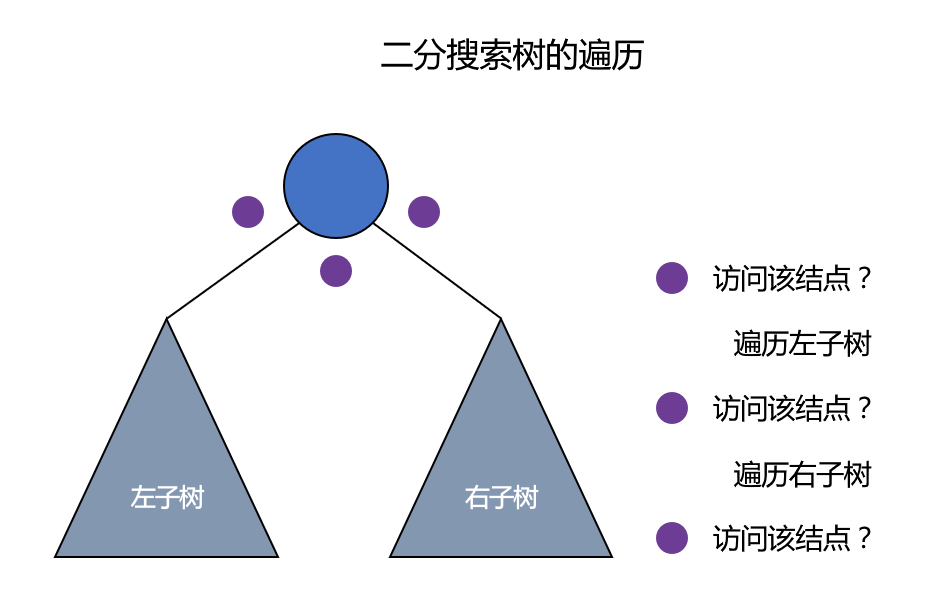
对于二叉树的每个节点(非空),都有 3 次访问机会,分别是访问该节点左子树之前;访问左子树和右子树之间;访问右子树之后。分别对应下图的 3 个紫色的点。更多关于二叉树的介绍可以参考之前的一篇博客:数据结构04-二分搜索树。
但对于 Morris 遍历,如果有左子树,那么它可以执行下面的代码:
1
2
3
4
5
6
|
process(root.left);
process(root.right);
|
如果没有左子树,那么只能执行下面的代码:
如果一个节点有左子树,使用 Morris 遍历可以访问该节点两次;如果一个节点没有左子树,使用 Morris 遍历之只能访问该节点一次。当第二次访问某个节点时,那么,该节点左子树必定已经全都访问过了。但无论如何,Morris 遍历无法做到第三次回到自身那个节点。
Morris 遍历是如何判断是第一次访问该节点还是第二次访问该节点呢?
对于递归来说,系统栈会记录执行到第几行,递归回来后,接着上次的继续执行;Morris 遍历则是根据当前节点左子树最右节点的右指针来判断,如果左子树上最右侧节点的右指针为 null,则是第一次访问当前节点;如果左子树上最右侧节点的右指针为 cur,则是第二次访问当前节点。
将上面算法流程用代码翻译下来就是 Morris 遍历:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
public void morris(TreeNode root) {
if (root == null) {
return;
}
TreeNode cur = root;
TreeNode mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight == null) {
mostRight.right = cur;
cur = cur.left;
continue;
} else {
mostRight.right = null;
}
}
cur = cur.right;
}
}
|
3. Morris 前中后序遍历
3.1 Morris 前序遍历
对照一般的递归方法的前序遍历,前序遍历是当第一次访问该节点的时候去处理该节点(这里是打印输出)。
1
2
3
4
5
6
7
8
9
10
|
public void preOrder(TreeNode root) {
if (root == null) {
return;
}
System.out.println(root.val);
preOrder(root.left);
preOrder(root.right);
}
|
对于 Morris 遍历来说,如果某个节点有左孩子,那么会访问该节点两次,在第一次访问时操作该节点;如果某个节点没有左孩子,只会访问该节点一次,就在访问到的时候操作该节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
public void morrisPreOrder(TreeNode root) {
if (root == null) {
return;
}
TreeNode cur = root;
TreeNode mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight == null) {
mostRight.right = cur;
System.out.println(cur.val);
cur = cur.left;
continue;
} else {
mostRight = null;
}
} else {
System.out.println(cur.val);
}
cur = cur.right;
}
}
|
3.2 Morris 中序遍历
同样对照递归中序遍历,递归版的中序遍历是在第二次访问该节点的时候操作该节点。
1
2
3
4
5
6
7
8
9
10
|
public void inOrder(TreeNode root) {
if (root == null) {
return;
}
inOrder(root.left);
System.out.println(root.val);
inOrder(root.right);
}
|
对于 Morris 遍历来说,如果某个节点有左孩子,那么会访问该节点两次,在第二次访问时操作该节点;如果某个节点没有左孩子,只会访问该节点一次,就在访问到的时候操作该节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
public void morrisInOrder(TreeNode root) {
if (root == null) {
return;
}
TreeNode cur = root;
TreeNode mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight == null) {
mostRight.right = cur;
cur = cur.left;
continue;
} else {
mostRight = null;
}
}
System.out.println(cur.val);
cur = cur.right;
}
}
|
3.3 Morris 后序遍历
递归的后续遍历,是在第三次访问该节点是对其进行操作。
1
2
3
4
5
6
7
8
9
10
|
public void postOrder(TreeNode root) {
if (root == null) {
return;
}
postOrder(root.left);
postOrder(root.right);
System.out.println(root.val);
}
|
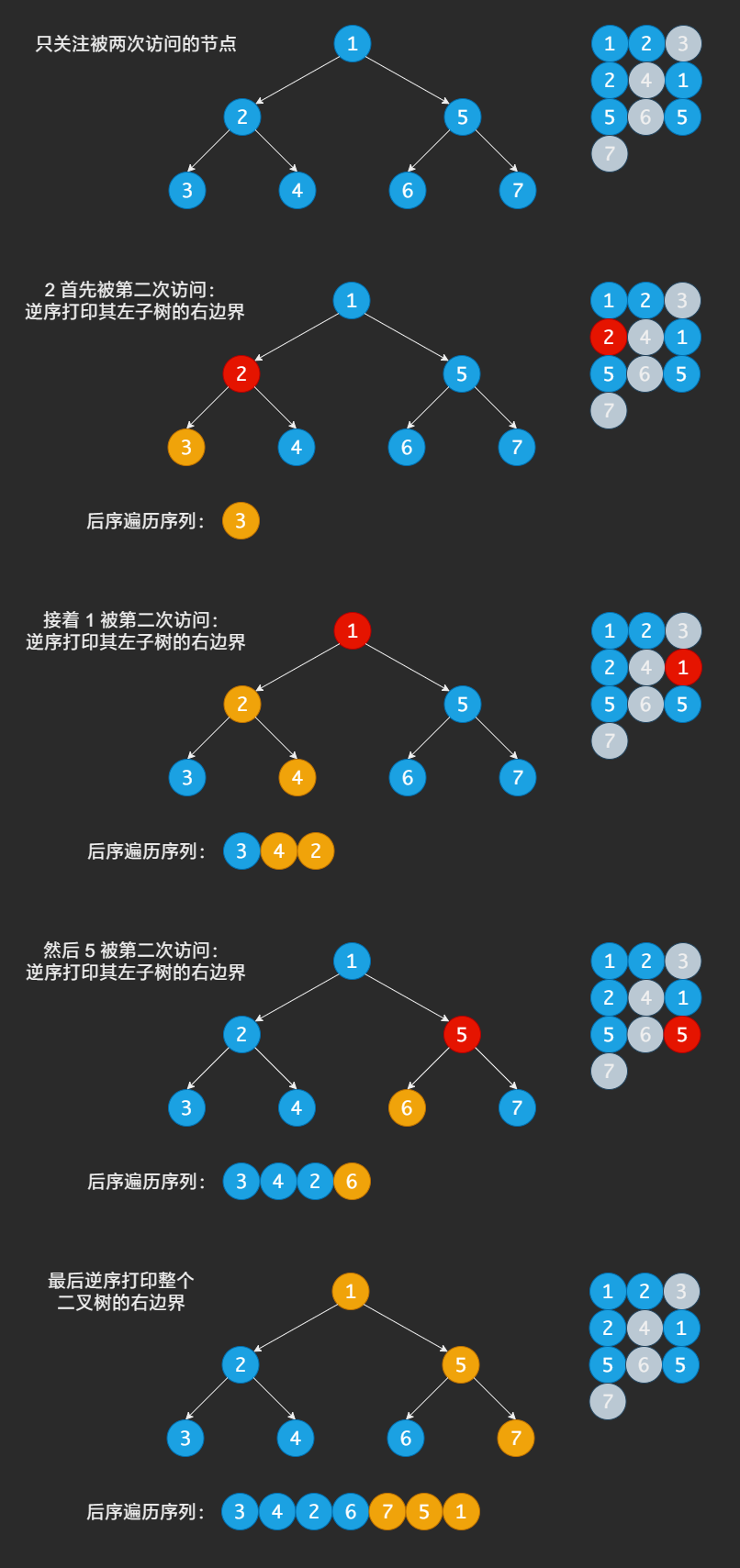
但 Morris 遍历无法三次访问一个节点,怎么做到后序遍历呢?
直接将具体做法:
对于 Morris 遍历,有的节点会被访问两次,有的节点会被访问一次,只关注会被访问两次的节点,当第二次访问该节点时,逆序操作其左子树的右边界,最后在函数退出之前,再单独逆序操作一次整棵树的右边界。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| public void morrisPostOrder(Node root) {
if (root == null) {
return;
}
TreeNode cur = root;
TreeNode mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) {
mostRight = mostRight.right;
}
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;
} else {
mostRight.right = null;
printRightEdge(cur.left);
}
}
cur = cur.right;
}
printRightEdge(root);
}
|
下面具体看 printRightEdge(TreeNode node) 函数的实现,printRightEdge(TreeNode node) 函数的功能是要逆序打印 node 的右边界(包含 node)。我们当然可以使用栈来辅助,但是使用栈又会占用额外空间。因此,将逆序打印右边界看成是对单链表的操作,先将右边界按照单链表逆序的方式逆序,打印完后,再逆序回来。
1
2
3
4
5
6
7
8
9
10
|
public void printRightEdeg(TreeNode head) {
TreeNode tail = reverseEdge(head);
TreeNode cur = tail;
while (cur != null) {
System.put.println(cur.val);
cur = cur.next;
}
reverseEdeg(tail);
}
|
1
2
3
4
5
6
7
8
9
10
11
12
|
public TreeNode reverseEdge(TreeNode from) {
TreeNode prev = null;
TreeNode next = null;
while (from != null) {
next = from.right;
from.right = prev;
prev = from;
from = next;
}
return prev;
}
|
4. 为什么时间复杂度是 O(N)
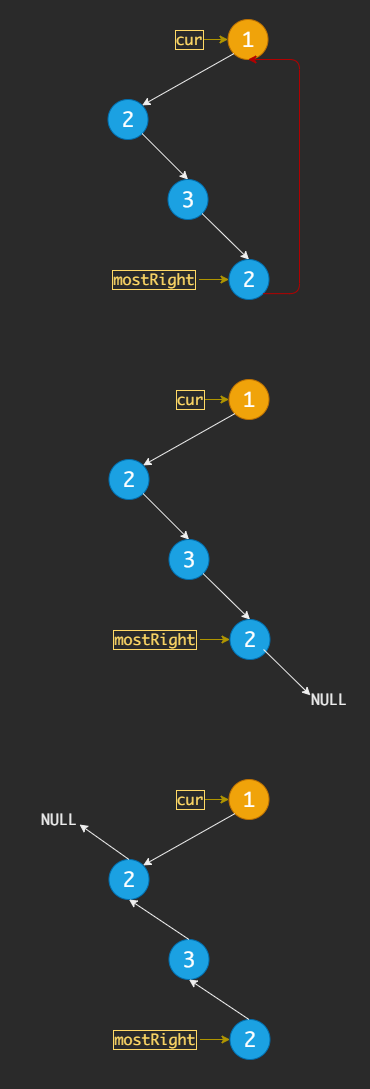
下面还是还原遍历的过程, cur → 1,mostRight → 2、4,表示当 cur 指向 1 这个节点时,mostRight 需要遍历的节点为 2、4。
cur → 1,mostRight → 2、4;
cur → 2,mostRight → 3;
cur → 3,mostRight → null;
cur → 2,mostRight → 3;
cur → 4,mostRight → null;
cur → 1,mostRight → 2、4;
cur → 5,mostRight → 6;
cur → 6,mostRight → null;
cur → 5,mostRight → 6;
cur → 7,mostRight → null;
cur → null。
首先,整棵二叉树可以被右边界划分,而对于一个节点,cur 最多会访问两次,每次访问,mostRight都会走一遍 cur 左子树的右边界,除了这两次遍历之外,这个右边界不会被再次遍历,也就是每个右边界只会被遍历有限次,而所有的右边界节点的总数又是 N,因此 Morris 遍历的时间复杂度还是 O(N)。
5. 问题
Morris 遍历会改变输入的数据的结构,因此如果要求不能该改变原本的树的结构,那么就不能使用 Morris 遍历。但是,这个算法真的是太 :cow: :beer:了!