数据结构04-二分搜索树

发表于 更新于 分类于 阅读次数： 评论数：

树（英语：tree）是一种抽象数据类型（ADT）或是实现这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。把它叫做“树”是因为它看起来像一棵倒挂的树。

二分搜索树（Binary Search Tree，BST）相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为 O(log n)。二分搜索树是基础性数据结构，用于构建更为抽象的数据结构。

维基百科

1. BST 基础

1.1 二叉树

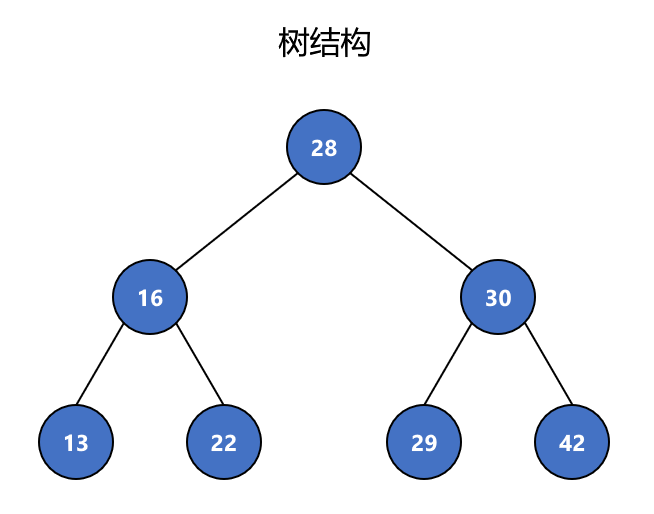
二叉树（Binary tree）是每个结点最多只有两个分支的树结构。通常分支被称作“左孩子”和“右孩子”或“左子树”和“右子树”。

二叉树的性质：

  • 二叉树只有一个根结点
  • 二叉树每个结点最多有两个孩子
  • 每个结点最多有一个父亲
  • 每个结点的左孩子也是一个二叉树
  • 每个结点的右孩子也是一个二叉树

二叉树不一定是“满”的，一个结点也是一个二叉树，NULL 也是一个二叉树。

1.2 BST

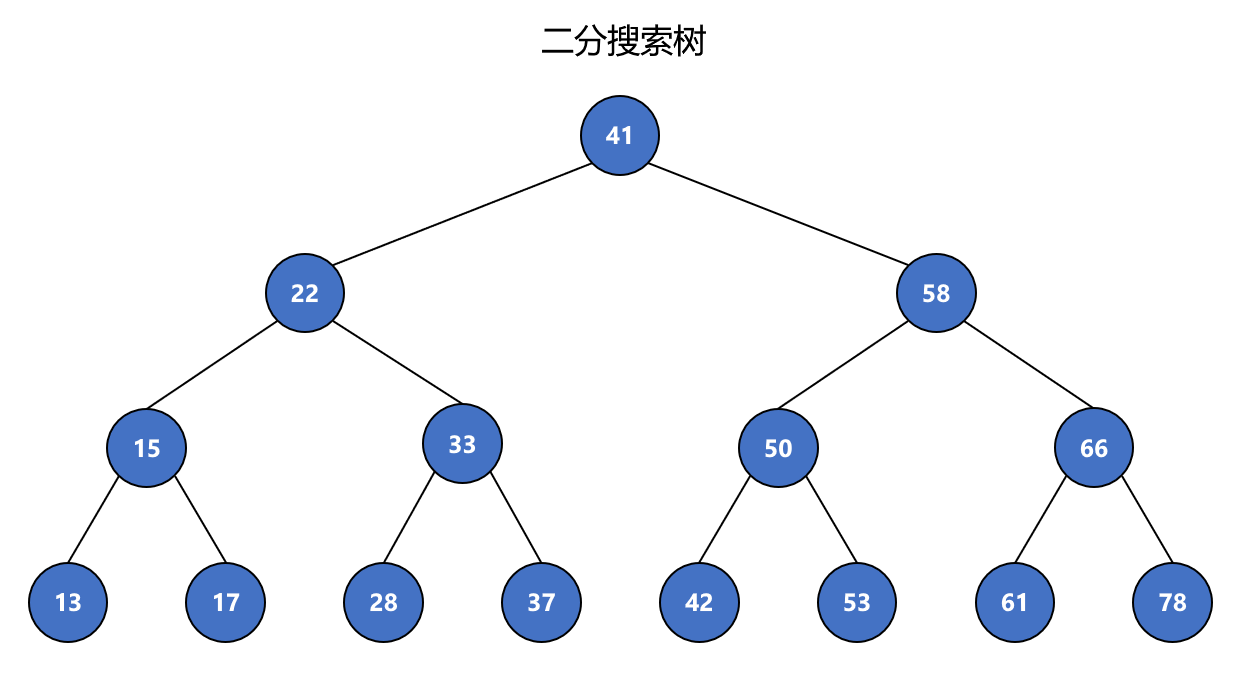
二分搜索树是一种二叉树，除了二叉树的性质之外，二分搜索树还有如下性质：

  • 二分搜索树中每个结点的值：
    • 大于其左子树的所有结点的值
    • 小于其右子树的所有结点的值
  • 任意结点的左、右子树也分别为二分搜索树

为了能达到搜索的目的，二分搜索树存储的元素必须有可比较性。

二分搜索树类中实现的方法：

方法 描述
int getSize() 获取二分搜索树中元素个数
boolean isEmpty() 返回二分搜索树是否为空
void add(E e) 向二分搜索树中添加新元素 e
boolean contains(E e) 查看二分搜索树中是否包含元素 e
E minimum() 查找二分搜索树的最小元素
E maximum() 查找二分搜索树的最大元素
void preOrder() 二分搜索树的前序遍历
void inOrder() 二分搜索树的中序遍历
void postOrder() 二分搜索树的后序遍历
void levelOrder() 二分搜索树的层序遍历
E removeMin() 从二分搜索树中删除最小值所在的结点，返回最小值
E removeMax() 从二分搜索树中删除最大值所在的结点，返回最大值
void remove(E e) 从二分搜索树中删除元素为 e 的结点

根据二分搜索树的性质，可以将结点信息以及简单的方法先完成。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public class BST<E extends Comparable<E>> {

    // 结点内部类
    private class Node {

        public E e;
        public Node left, right;

        public Node(E e) {
            this.e = e;
            this.left = null;
            this.right = null;
        }
    }

    private Node root;
    private int size;

    public BST() {
        this.root = null;
        this.size = 0;
    }

    public int getSize() {
        return size;
    }

    public boolean isEmpty() {
        return size == 0;
    }    
}

2. 向 BST 中添加元素

方法 描述
void add(E e) 向二分搜索树中添加新元素 e

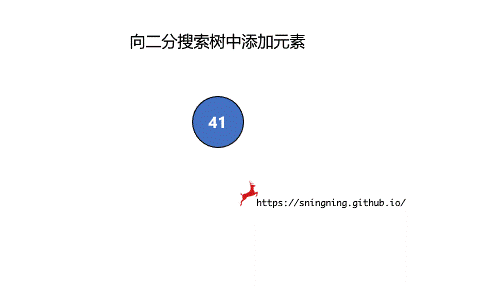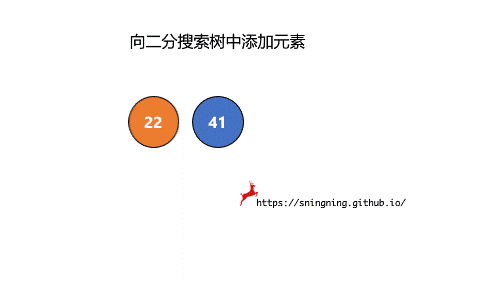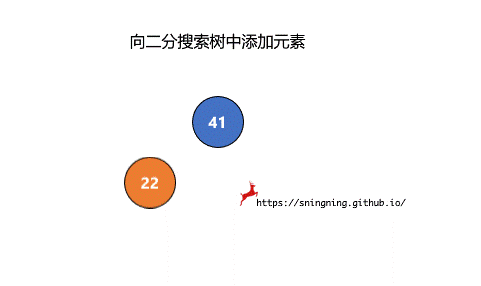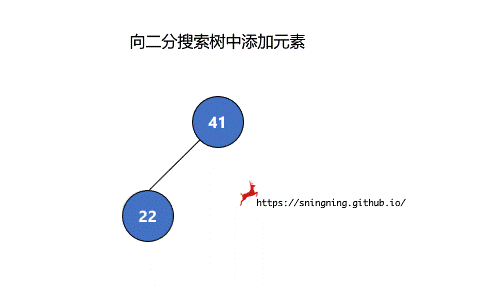
如果当前的二分搜索树为空，那么直接可以将新的元素添加，同时维护 size。

如果当前二分搜索树不为空，那么需要从根结点出发，先与根结点比较。

  • 比根结点大，往右子树插入；
  • 比根结点小，往左子树插入；
  • 和根结点相等，不做改变；（实现的二分搜索树不包含重复元素）

这样依次递归下去，知道要插入的位置为空，那么就可以将该元素正确地添加到树中。因此可以写一个递归的方法来实现添加元素的操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
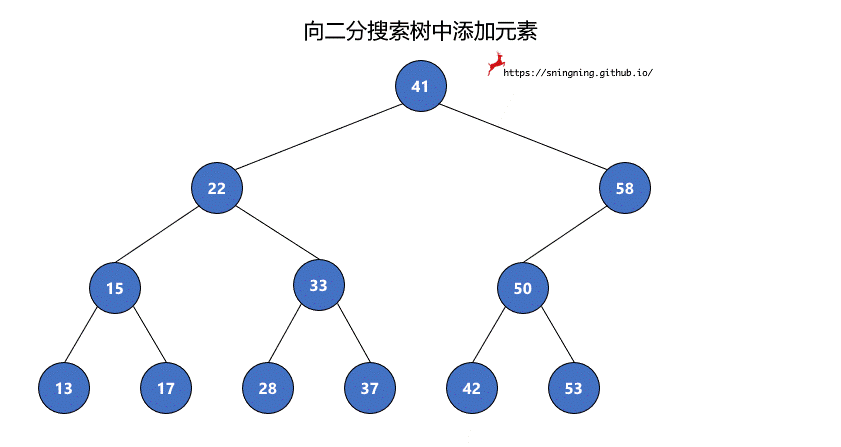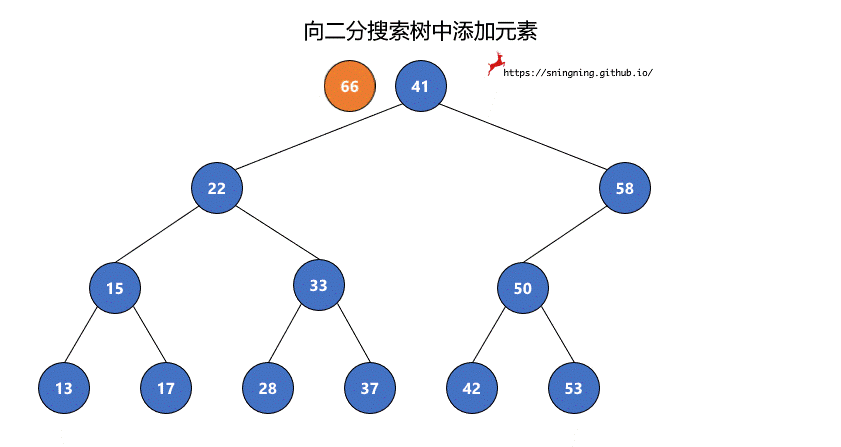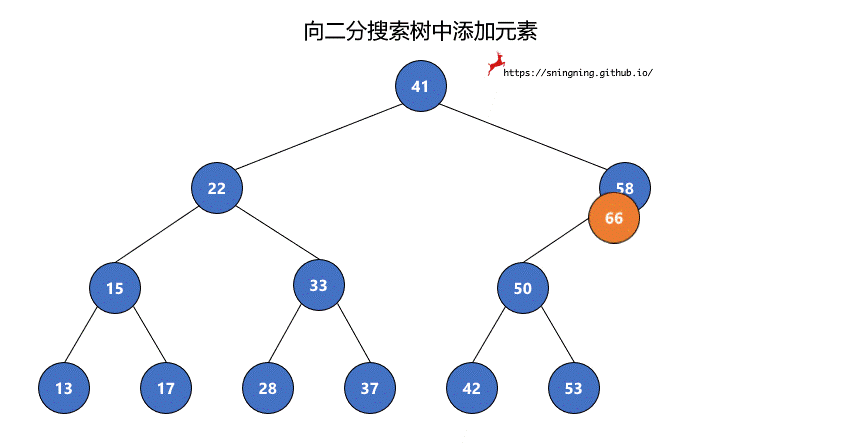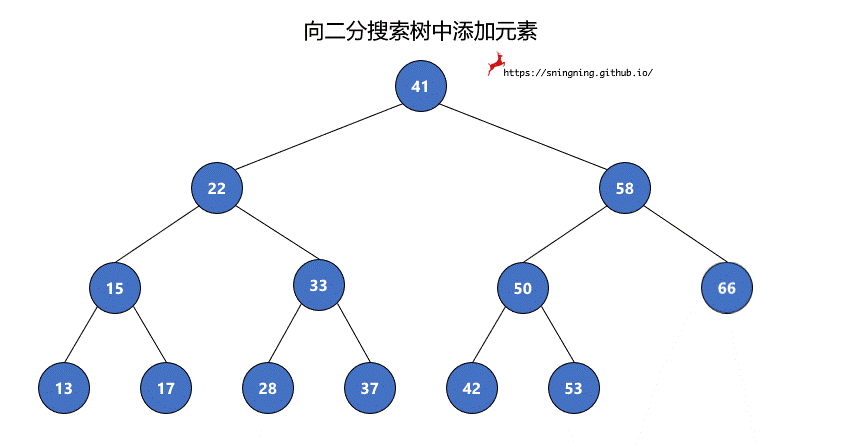
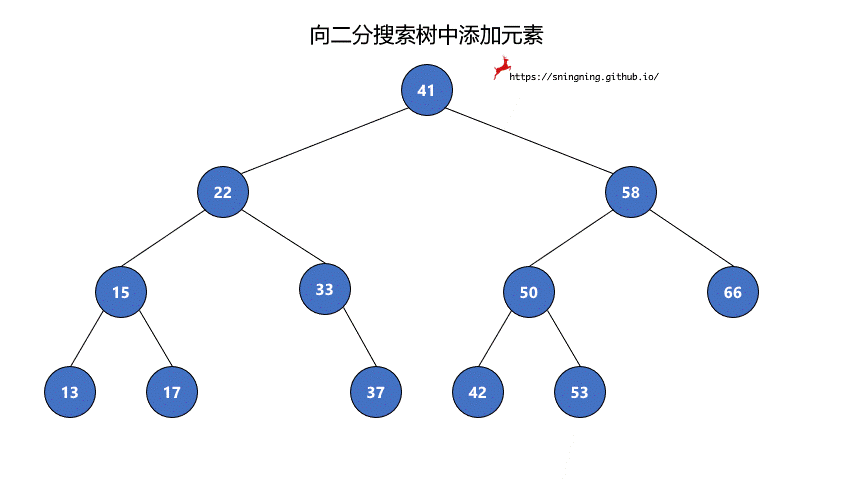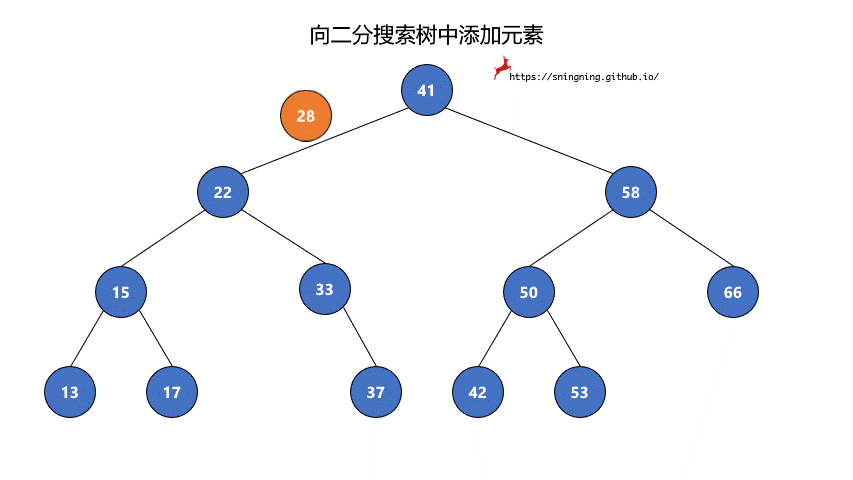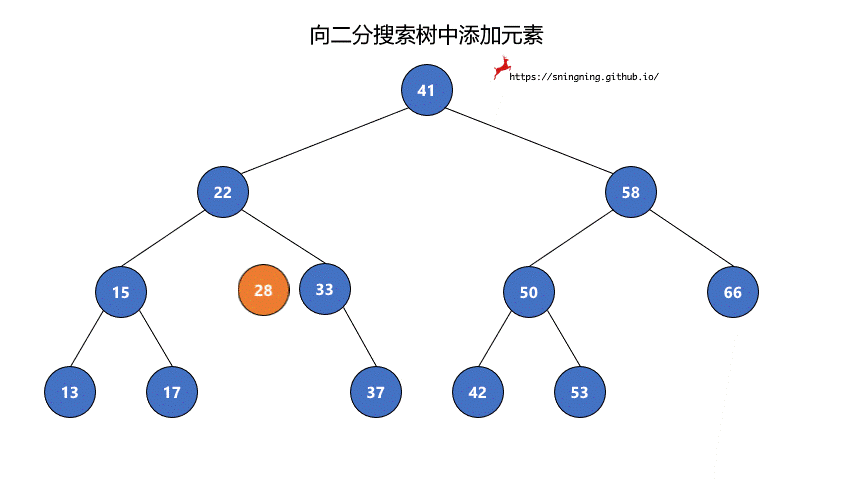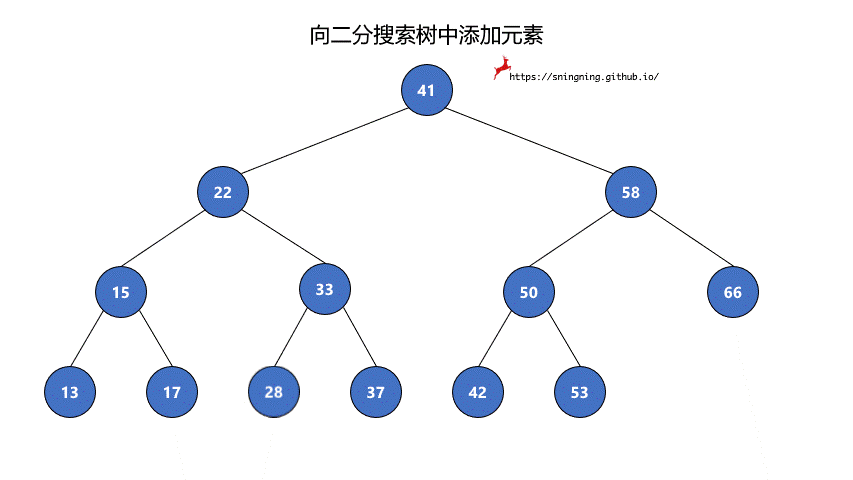
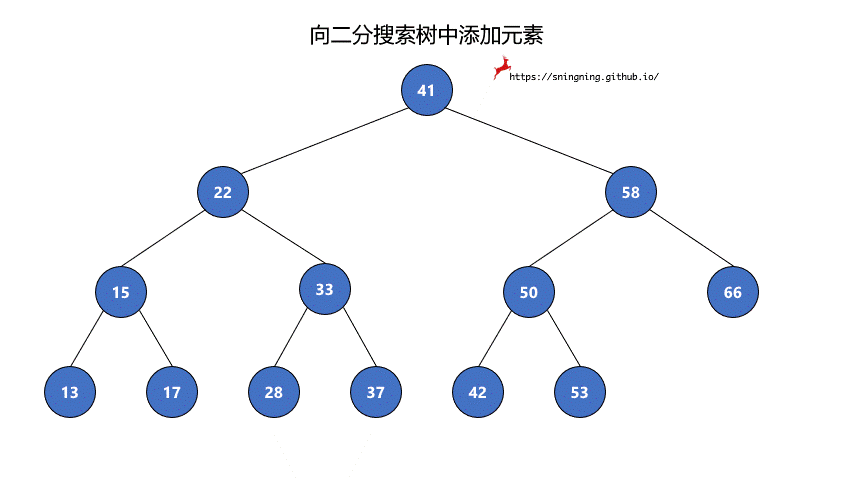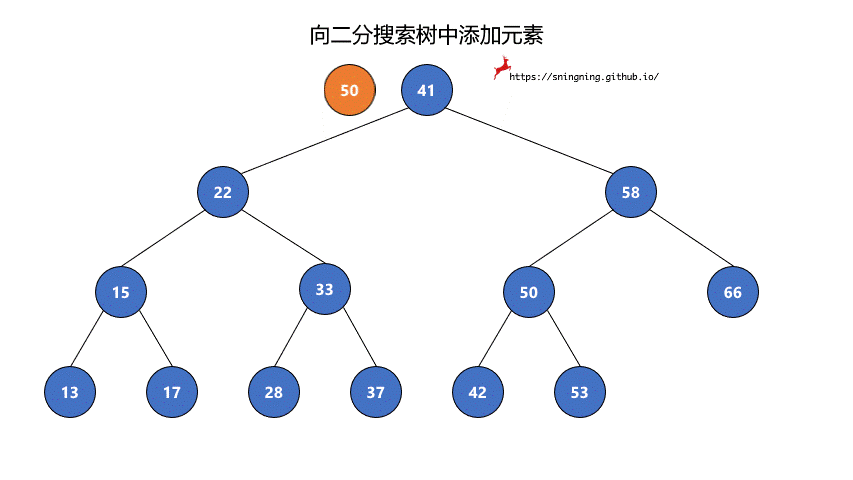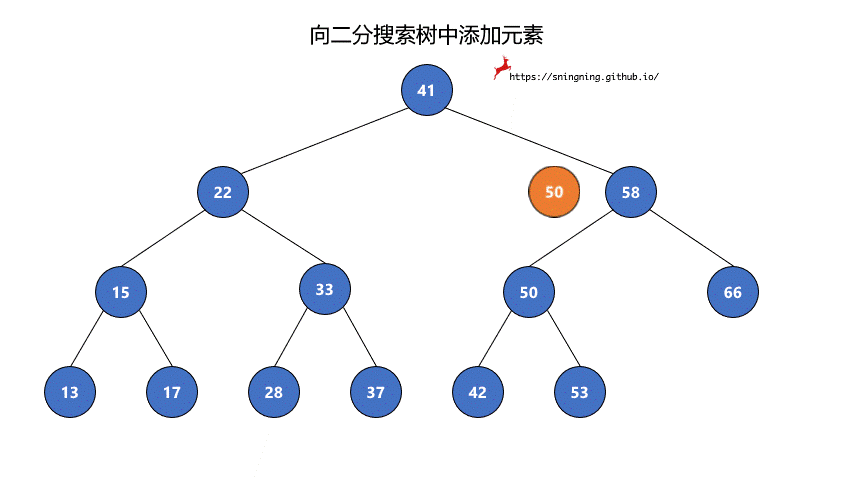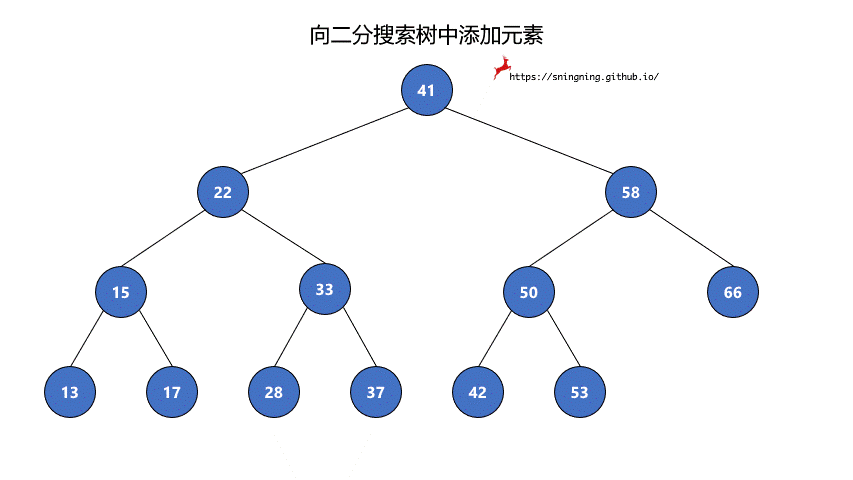
37
// 向二分搜索树中添加新元素 e
public void add(E e) {

    if (root == null) {
        root = new Node(e);
    }
    else {
        add(root, e)
    }
}

// 向以 node 为根的二分搜索树中插入元素 e，递归算法
private void add(Node node, E e) {

    // 递归终止的条件
    if(e.equals(node.e)) {
        return;
    }
    else if (e.compareTo(node.e) < 0 && node.left == null) {
        node.left = new Node(e);
        size++;
        return;
    }
    else if (e.compareTo(node.e) > 0 && node.right == null) {
        node.right = new Node(e);
        size++;
        return;
    }

    // 递归过程
    if(e.compareTo(node.e) < 0) {
        add(node.left, e);
    }
    else {  //e.compareTo(node.e) > 0
        add(node.right, e);
    }
}

3. 改进添加操作

前面实现的添加操作中，对于 root == null 的情况进行了单独处理，但是提到过，null 也是一个二分搜索树。因此，如果待插入的元素走到了一个 null 的位置，肯定要在这里新创建一个结点。

所以将之前递归代码的终止条件中，左右子树为空的条件去掉，让待插入元素再递归一层走到 null，和之前的递归过程相比，相当于多递归了一层，在 null 这个位置新建结点插入，然后将插入结点后的树返回给上一层递归调用，让进入递归前该结点的左子树或右子树接住这个变化，这样完成整个二分搜索树的更新。

如果待插入的元素和某一个结点元素相等，就直接将该结点返回给上层调用就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// 向二分搜索树中添加新元素 e
public void add(E e) {
    add(root, e);
}

// 向以 node 为根的二分搜索树中插入元素 e，递归算法
// 返回插入新结点后二分搜索树的根
private Node add(Node node, E e) {

    // 递归终止的条件
    if (node == null) {
        size++;
        return new Node(e);
    }

    if (e.compareTo(node.e) < 0) {
        node.left = add(node.left, e);
    }
    else if(e.compareTo(node.e) > 0) {
        node.right = add(node.right, e);
    }

    // 如果 e.equals(node.e)，上面代码不执行，直接将该结点返回

    return node;

}

4. BST 的查询操作

二分搜索树的查询操作，分为查询指定元素 e 是否存在；查询树中最大元素和最小元素。

方法 描述
boolean contains(E e) 查看二分搜索树中是否包含元素 e
E minimum() 查找二分搜索树的最小元素
E maximum() 查找二分搜索树的最大元素

4.1 查询指定元素

要实现在二分搜索树中查询某个特定的元素是否存在，给定元素后，先与根结点比较，后续过程和添加元素操作一样，因此也可以使用递归来实现。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 查看二分搜索树中是否包含元素 e
public boolean contains(E e) {
    return contains(node, e);
}

// 查看以 node 为根的二分搜索树中是否包含元素 e，递归算法
private boolean contains(Node node, E e) {

    // 递归终止的条件
    if (node == null) {
      return false;
    }

    if (e.equals(node.e)) {
        return true;
    }
    else if (e.compareTo(node.e) < 0) {
        return contains(node.left, e);
    }
    else {
        return contains(node.right, e);
    }
}

4.2 查询最小元素和最大元素

根据二分搜索树的性质，当沿着树的左子树一直往下寻找，当到达最左端，也就是结点的左子树为空时，该结点中存储的元素就是整个树中的最小元素，最大元素相反，往右一直寻找。因此，寻找最小元素和最大元素的过程也是递归进行的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 寻找二分搜索树的最小元素
public E minimum() {

    if (size == 0) {
        throw new IllegalArgumentException("树为空。");
    }

    return minimum(root).e;
}

// 返回以 node 为根的二分搜索树的最小键值所在的结点
private Node minimum(Node node) {

    // 递归终止的条件
    if (node.left == null) {
        return node;
    }

    return minimum(node.left);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 寻找二分搜索树的最大元素（递归实现）
public E maximum() {

    if (size == 0) {
        throw new IllegalArgumentException("树为空。");
    }

    return maximum(root).e;
}

// 返回以 node 为根的二分搜索树的最大键值所在的结点
private Node maximum(Node node) {

    if (node.right == null) {
        return node;
    }

    return maximum(node.right);
}

在二分搜索树中寻找最小值和最大值的过程其实和对一个链表进行遍历是一样的操作，因此完全可以使用一个循环来找到相应的最小值和最大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 寻找二分搜索树的最小元素（非递归实现）
public E minimumNR() {

    if (size == 0) {
        throw new IllegalArgumentException("树为空。");
    }

    Node cur = root;
    while (cur.left != null) {
        cur = cur.left;
    }

    return cur.e;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 寻找二分搜索树的最大元素（非递归实现）
public E maximumNR() {

    if (size == 0) {
        throw new IllegalArgumentException("树为空。");
    }

    Node cur = root;
    while (cur.right != null) {
        cur = cur.right;
    }

    return cur.e;
}

5. BST 的前、中、后序遍历

方法 描述
void preOrder() 二分搜索树的前序遍历
void inOrder() 二分搜索树的中序遍历
void postOrder() 二分搜索树的后序遍历

与添加和查询操作不同，二分搜索树的遍历操作要将二分搜索树所有的结点都访问一遍，而非仅仅是左子树或右子树。

运用递归操作，依然可以方便地对二分搜索树进行遍历操作。用递归方法遍历以 node 为根的二分搜索树，整体思路如下：

  • 开始：
    • node 为空：直接返回
    • node 不为空：
      • 访问 node
      • 遍历 node.left
      • 遍历 node.right
  • 结束

其中，递归调用发生在遍历左子树和右子树的操作中。根据访问 node 的顺序不同，遍历可以分为前序遍历、中序遍历、后序遍历。这里定义访问 node 的操作为打印 node 结点存储的元素。


5.1 前序遍历

最主要的是实现遍历的递归函数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 二分搜索树的前序遍历
public void preOrder() {
    preOrder(root);
}

// 前序遍历以 node 为根的二分搜索树，递归算法
private void preOrder(Node node) {

    // 递归终止条件
    if (node == null) {
        return;
    }

    System.out.println(node.e);
    preOrder(node.left);
    preOrder(node.right);
}

5.2 中序遍历

中序遍历无非是把访问该结点信息的操作放在访问左子树和右子树中间，根据二分搜索树的性质可以知道，该结点左子树均是小于该结点的，右子树都是大于该结点的，因此，二分搜索树中序遍历的结果是顺序的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 二分搜索树的中序遍历
public void inOrder() {
    inOrder(root);
}

// 中序遍历以 node 为根的二分搜索树，递归算法
private void inOrder(Node node) {

    // 递归终止条件
    if (node == null) {
        return;
    }

    inOrder(node.left);
    System.out.println(node.e);
    inOrder(node.right);
}

5.3 后序遍历

后序遍历就是先访问该结点的左子树，再访问该结点的右子树，最后访问该结点。后序遍历的一个应用就是释放二分搜索树的内存，如果手动释放内存，就需要先将孩子结点的内存释放，最后再释放该结点的内存。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// 二分搜索树的后序遍历
public void postOrder() {
    postOrder(root);
}

// 后序遍历以 node 为根的二分搜索树，递归算法
private void postOrder(Node node) {

    // 递归终止条件
    if (node == null) {
        return;
    }

    postOrder(node.left);
    postOrder(node.right);
    System.out.println(node.e);
}

5.4 再理解 BST 的遍历

对于二分搜索树的遍历，程序编写是简单的，但是如果面对一颗二分搜索树，怎样快速手写出前中后序遍历结果？

对于二分搜索树的每个结点，都有 3 次访问机会，分别是访问该结点左子树之前；访问左子树和右子树之间；访问右子树之后。分别对应下图的 3 个紫色的点。


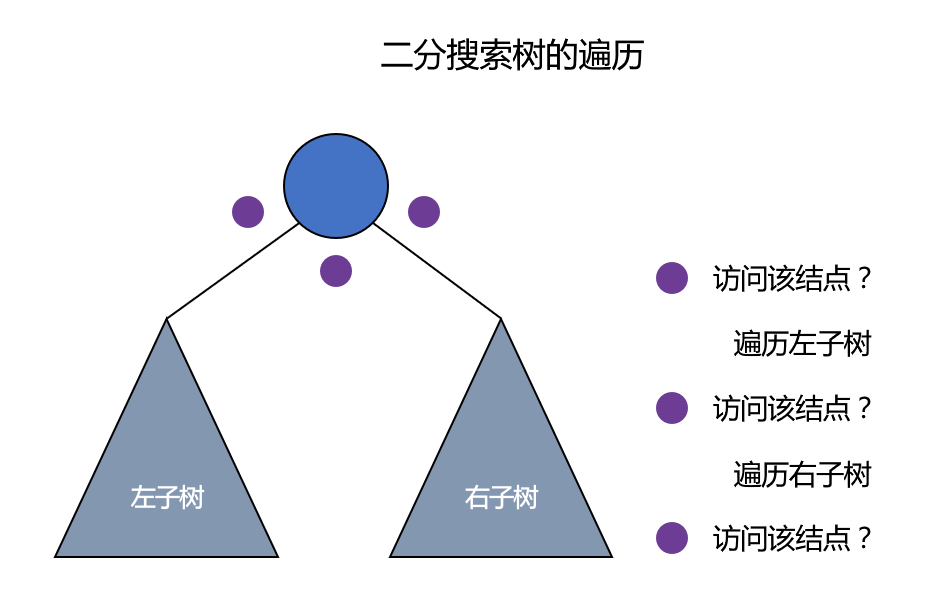
前序遍历过程中，真正打印该结点是在第 1 次访问该结点的时候。


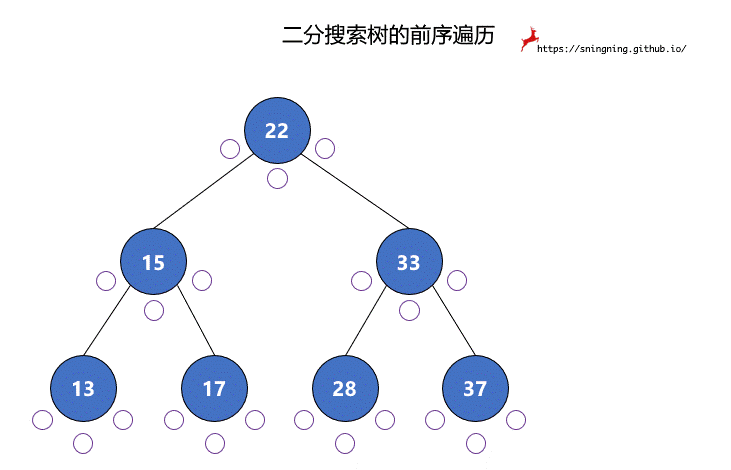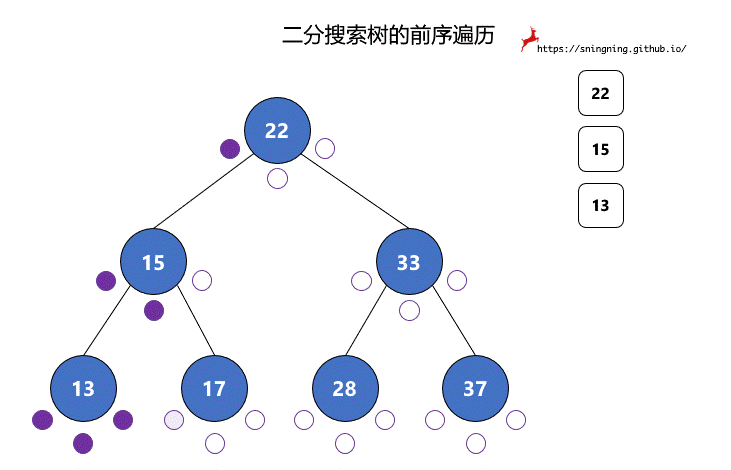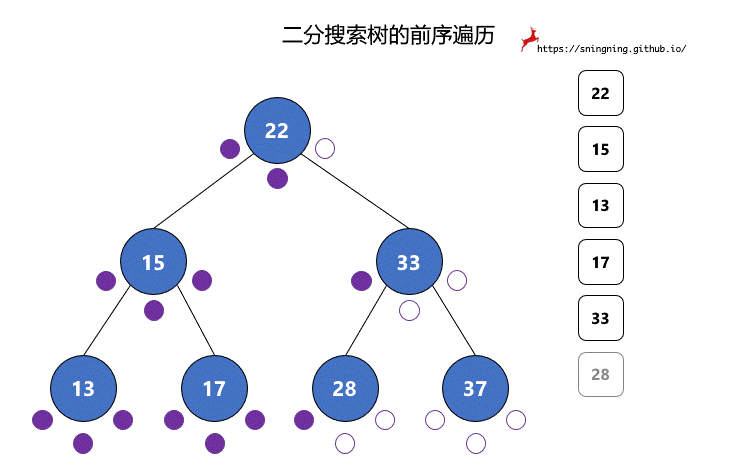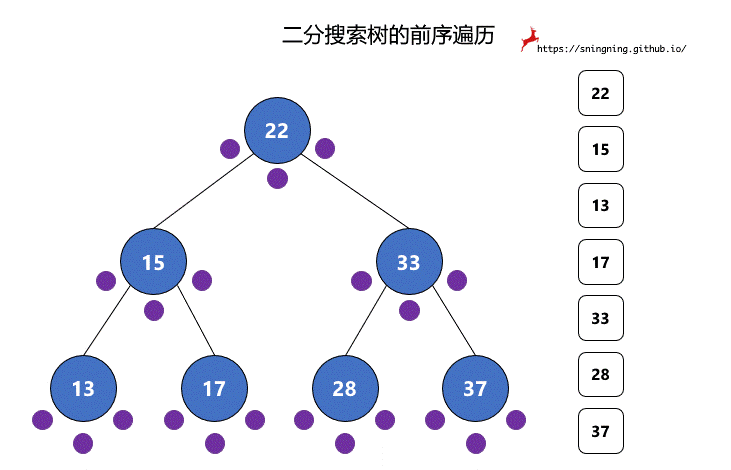
中序遍历过程中，真正打印该结点是在第 2 次访问该结点的时候。


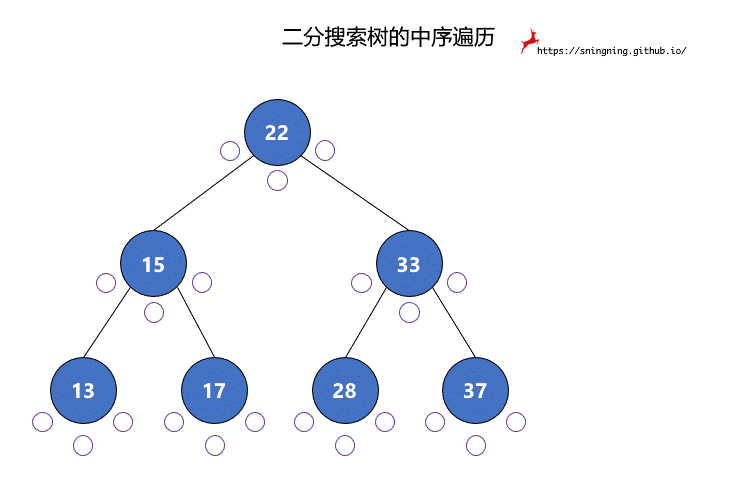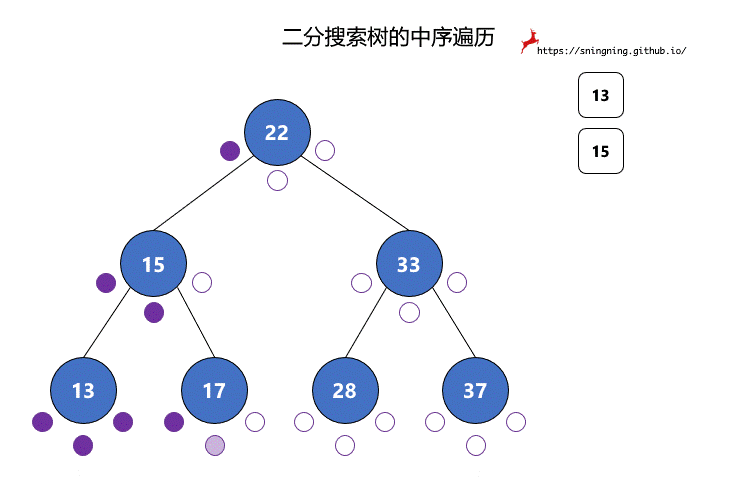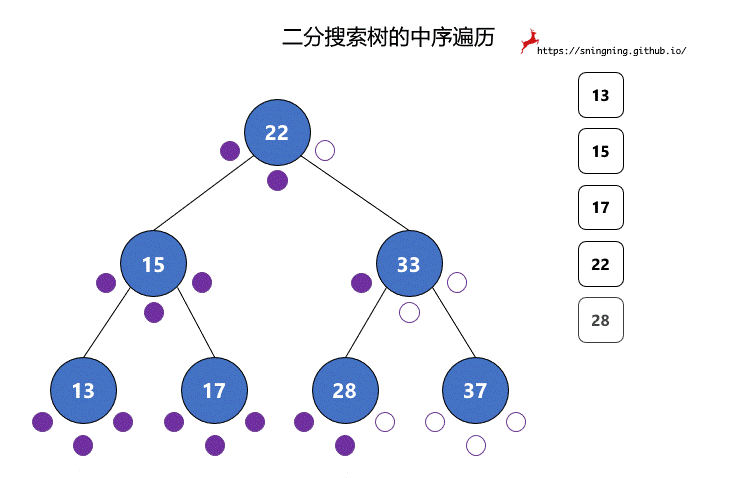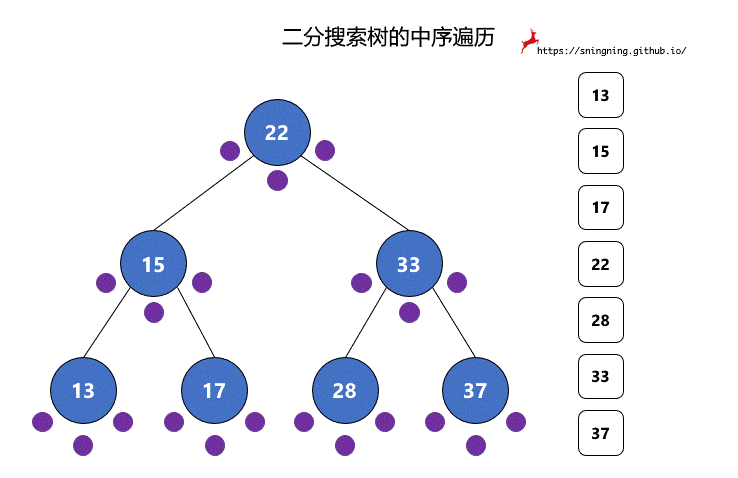
后序遍历过程中，真正打印该结点是在第 3 次访问该结点的时候。

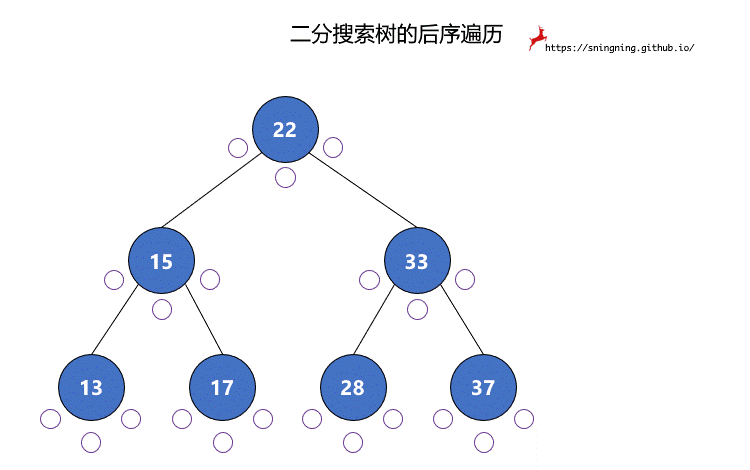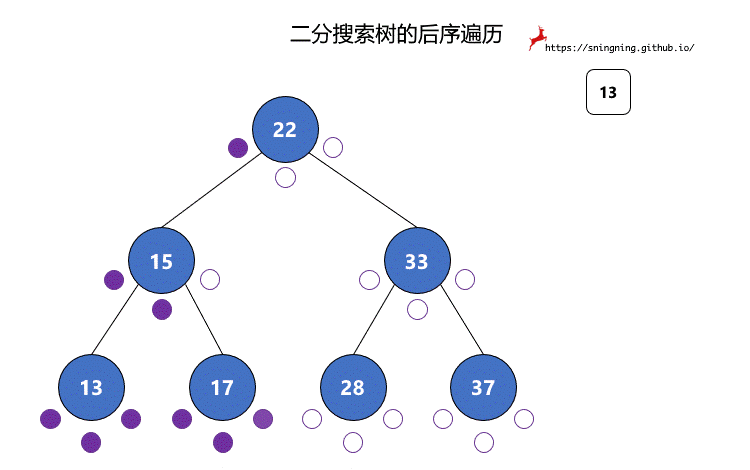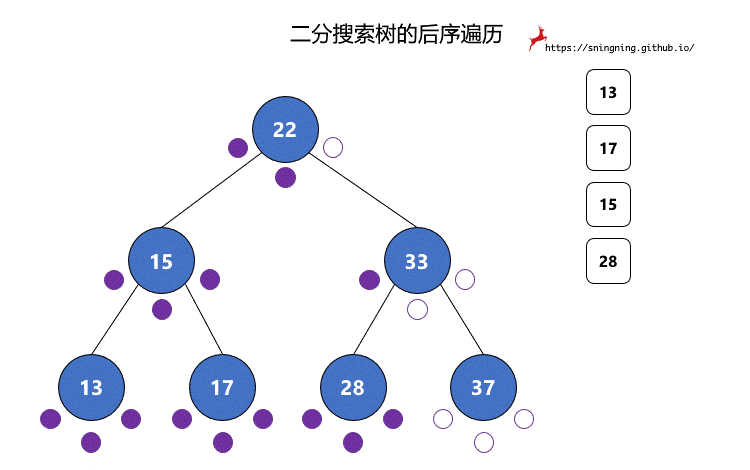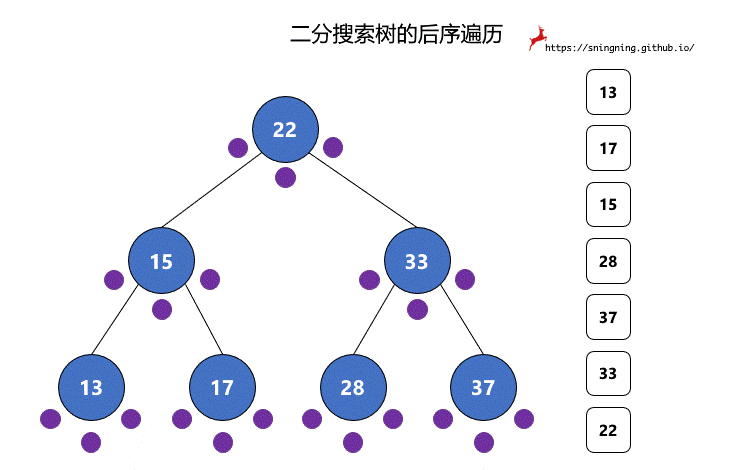
6. BST 前序遍历的非递归实现

利用栈来实现前序遍历，根据栈结构后入先出的性质，栈顶元素是要访问的元素，先访问该元素，然后将该元素弹出栈，随后将该结点的孩子压入栈，入栈顺序是右孩子先入栈，然后左孩子再入栈，这样，栈顶元素就是左孩子，然后访问左孩子，弹出栈，再依次压入它的右孩子和左孩子，依次进行。当栈为空时，完成遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 二分搜索树的非递归前序遍历，非递归实现
public void preOrderNR() {

    Deque<Node> stack = new LinkedList<>();
    stack.push(root);
    while (!stack.isEmpty()) {

        Node cur = stack.pop();
        System.out.println(cur.e);

        if (cur.right != null) {  // 右孩子先入栈
            stack.push(cur.right);
        }
        if (cur.left != null) {
            stack.push(cur.left); 
        }
    }
}

7. BST 的层序遍历

方法 描述
void levelOrder() 二分搜索树的层序遍历

二分搜索树的前中后序遍历都是在树的一侧一插到底，然后往回递归。层序遍历就是对于一个树，一层一层地对每个结点进行操作，层序遍历又称为广度优先遍历，相对应的，二分搜索树的前中后序遍历又称为深度优先遍历。对于二分搜索树的层序遍历，多是使用非递归实现，这里使用队列这种数据结构来实现二分搜索树的层序遍历。

队首元素是当前需要操作的元素，将队首元素出队，操作完成后，将该元素的左孩子和右孩子依次入队，知道队列为空，此时完成层序遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 二分搜索树的层序遍历（广度优先遍历）
public void levelOrder() {

    Queue<E> queue = new LinkedList<>();
    queue.offer(root);
    while (!queue.isEmpty()) {

        Node cur = queue.poll();
        System.out.println(cur.e);

        if (cur.left != null) {  // 左孩子先入队
            queue.offer(cur.left);
        }
        if (cur.right != null) { // 右孩子再入队
            queue.offer(cur.right); 
        }
    }
}

广度优先遍历有时可以更快的找到指定的元素，如下图所示，当要找的元素在红点位置，但使用深度优先遍历会直接先插到底部从左边寻找，而这是如果采用广度优先遍历便可以很快找到答案。

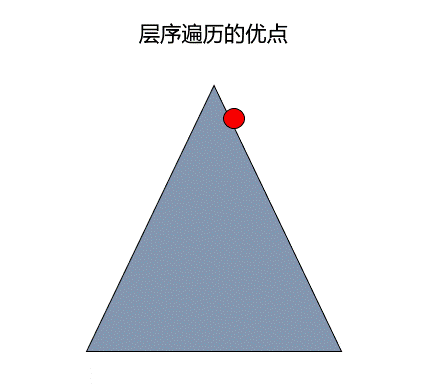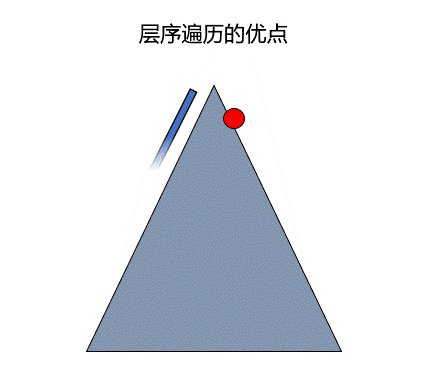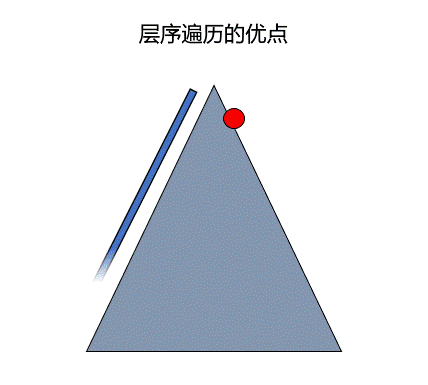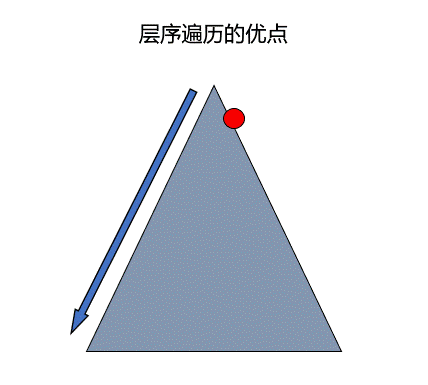
在图中也存在深度优先遍历和广度优先遍历，不过在图中进行遍历时，需要记录一下该结点之前是否遍历过，因为对于图来说，每一个结点的前驱可能有多个。

8. 删除 BST 中最小元素和最大元素

方法 描述
E removeMin() 从二分搜索树中删除最小值所在的结点，返回最小值
E removeMax() 从二分搜索树中删除最大值所在的结点，返回最大值

最小元素和最大元素所在的结点可能是叶子结点也可能不是叶子结点。

8.1 删除 BST 中最小元素

如果最小元素所在的结点是叶子结点，可以直接将其删除。但是当待删除的结点有右子树时，将该结点删除后，还要再把其右子树赋给其父亲结点，也就是该结点左子树的根结点接替了该结点的位置。由于 null 也可以看做一个结点，因此，两个过程可以统一。最后维护 size。这里复用了之前的 minmum() 方法，因此不需要再对空树进行判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
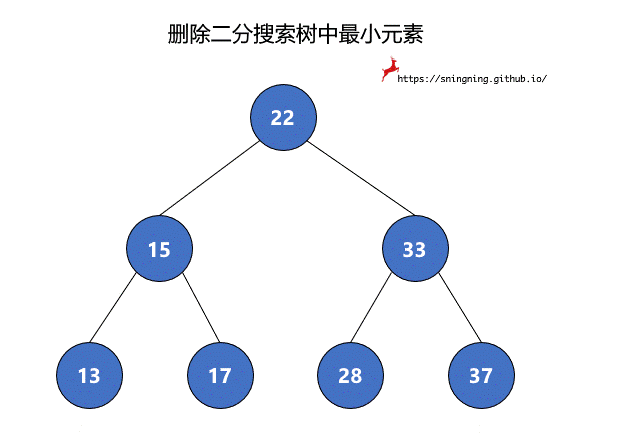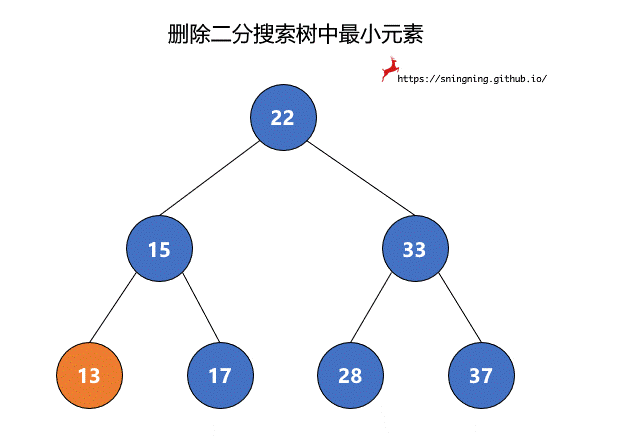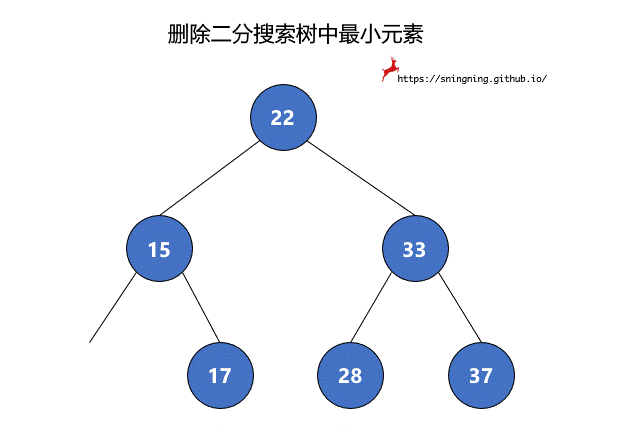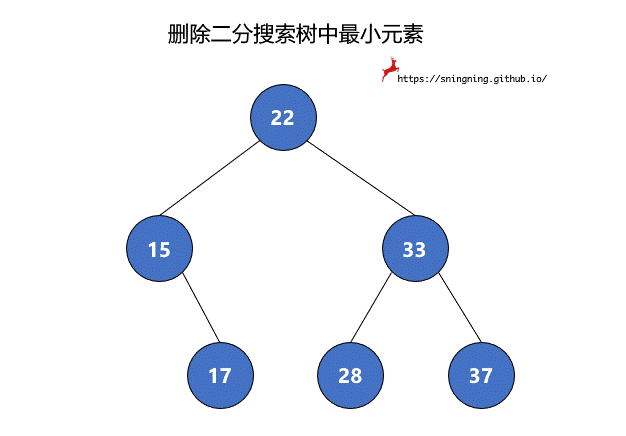
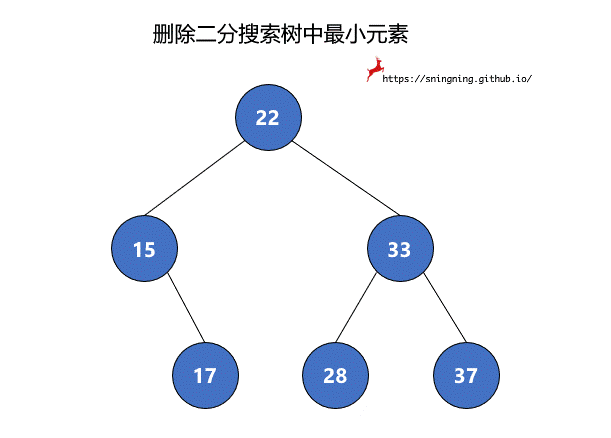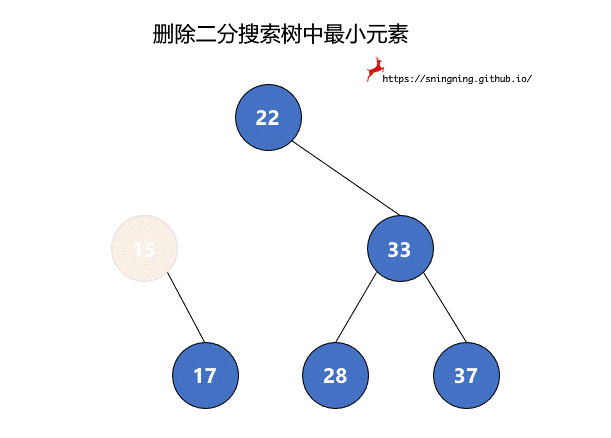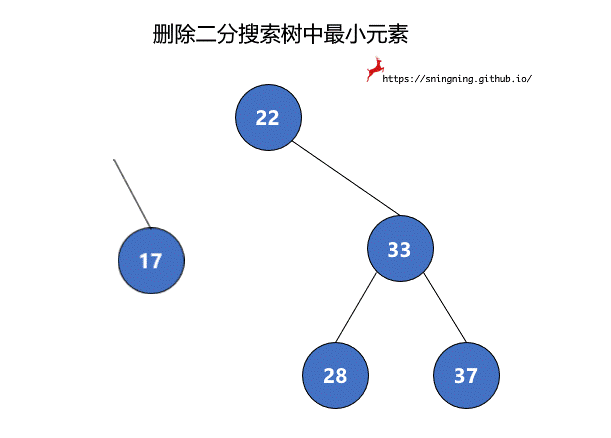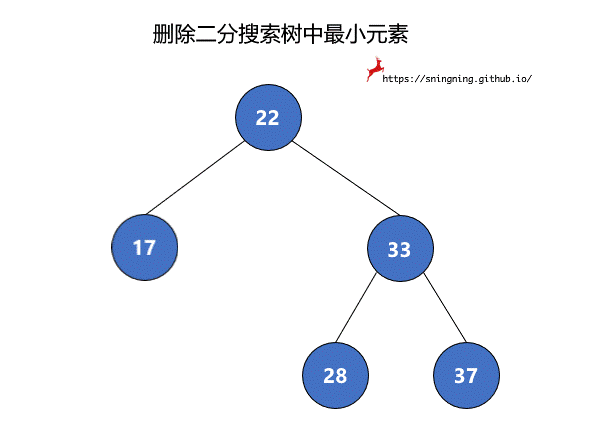
24
// 从二分搜索树中删除最小值所在的结点，返回最小值
public E removeMin() {

    E ret = minmum();
    root = removeMin(root);
    return ret;
}

// 删除掉以 node 为根的二分搜索树中的最小结点
// 返回删除结点后新的二分搜索树的根
private Node removeMin(Node node) {

    // 递归终止条件
    if (node.left == null) {

        Node rightNode = node.right;
        node.right = null;
        size--;
        return rightNode;
    }

    node.left = removeMin(node.left);
    return node;
}

8.2 删除 BST 中最大元素

删除最大元素和删除最小元素刚好相反，只需保存待删除结点的左子树即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 从二分搜索树中删除最大值所在的结点，返回最大值
public E removeMax() {

    E ret = maximum();
    root = removeMax(root);
    return ret;
}

// 删除掉以 node 为根的二分搜索树中的最大结点
// 返回删除结点后新的二分搜索树的根
private Node removeMax(Node node) {

    if (node.right == null) {

        Node leftNode = node.left;
        node.left = null;
        size--;
        return leftNode;
    }

    node.right = removeMax(node.right);
    return node;
}

9. 删除 BST 中任意元素

方法 描述
void remove(E e) 从二分搜索树中删除元素为 e 的结点

删除任意元素时，也是分成 3 种情况：

  • 待删除元素所在结点左子树为空
  • 待删除元素所在结点右子树为空
  • 待删除元素所在结点左右子树都存在

前两种情况和删除最小元素和最大元素是类似：
如果左子树为空，暂存右子树，将该结点删除，然后将右子树的根结点返回给上一层递归调用；
如果右子树为空，暂存左子树，将该结点删除，然后将左子树的根结点返回给上一层递归调用。

当待删除元素所在结点左右子树都存在时，这里采用Hibbard Deletion。

Delete. We can proceed in a similar manner to delete any node that has one child (or no children), but what can we do to delete a node that has two children? We are left with two links, but have a place in the parent node for only one of them. An answer to this dilemma, first proposed by T. Hibbard in 1962, is to delete a node x by replacing it with its successor. Because x has a right child, its successor is the node with the smallest key in its right subtree. The replacement preserves order in the tree because there are no keys between x.key and the successor’s key. We accomplish the task of replacing x by its successor in four (!) easy steps:

  • Save a link to the node to be deleted in t
  • Set x to point to its successor min(t.right).
  • Set the right link of x (which is supposed to point to the BST containing all the keys larger than x.key) to deleteMin(t.right), the link to the BST containing all the keys that are larger than x.key after the deletion.
  • Set the left link of x (which was null) to t.left (all the keys that are less than both the deleted key and its successor).

Algorithms(4th edition) P410

再来几个动画演示。


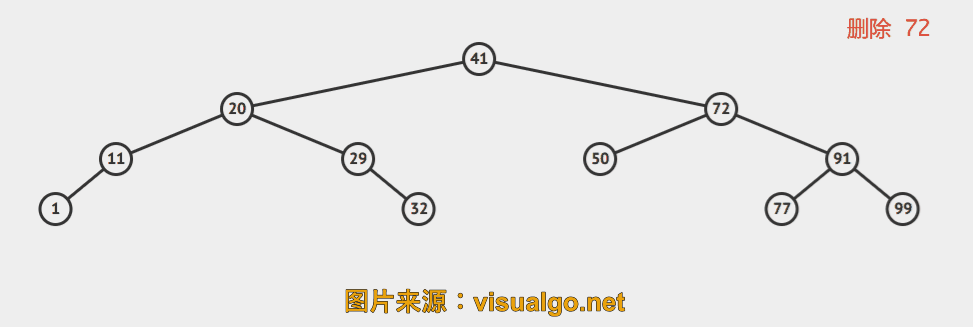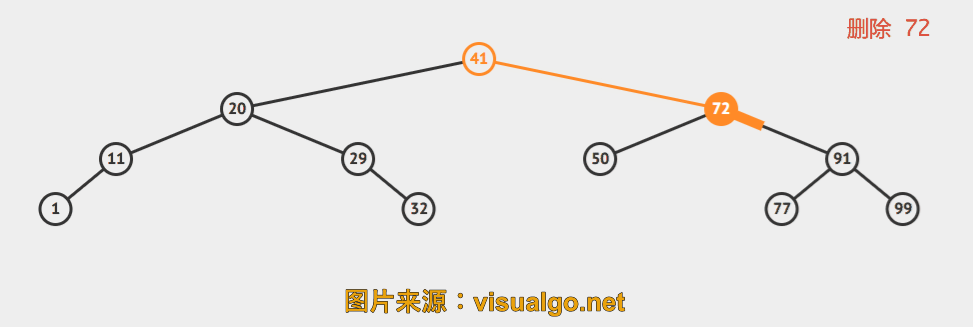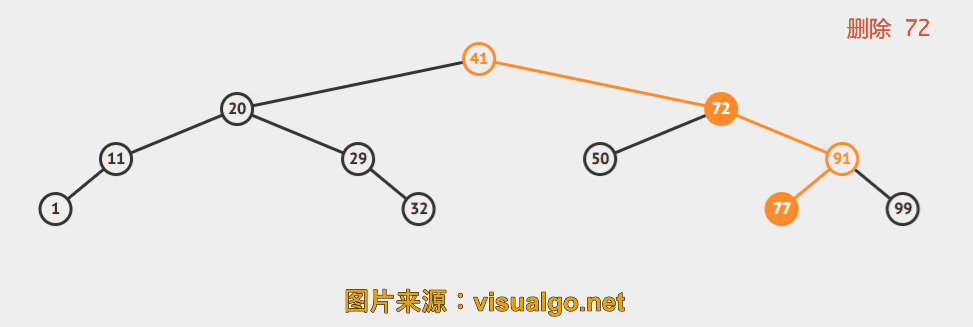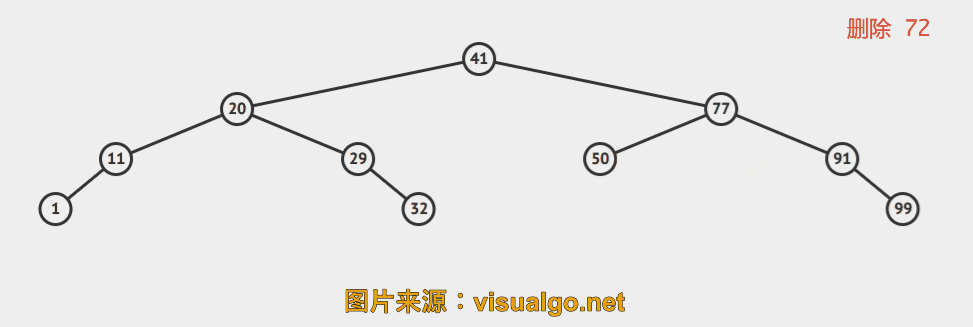
一句话概括就是，找到待删除结点右子树中的最小值所在结点，用此结点接替待删除的结点。简单描述下过程：

d 为待删除结点

  • 找到 s = min( s->right ), s 是 d 的后继
  • s->right = delMin( d->right )
  • s->left = d->left
  • 删除 d, s 是新的子树的根
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
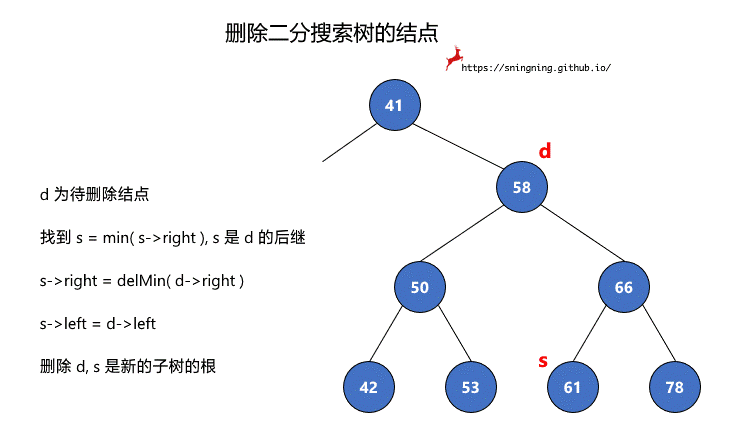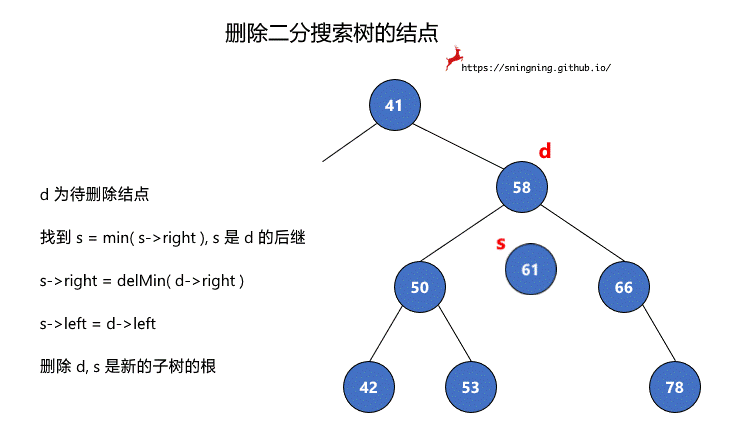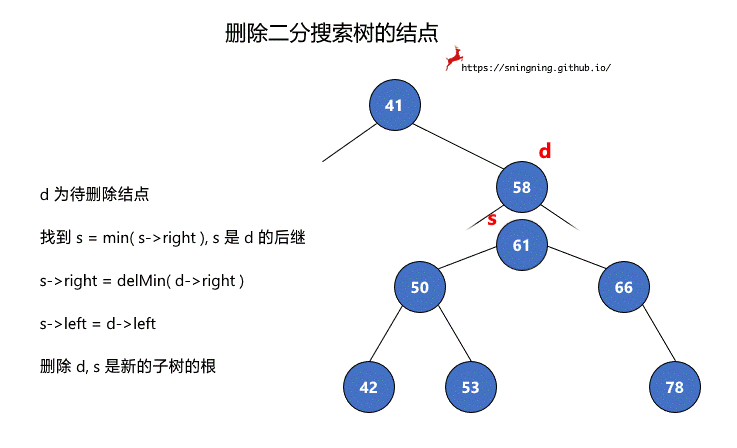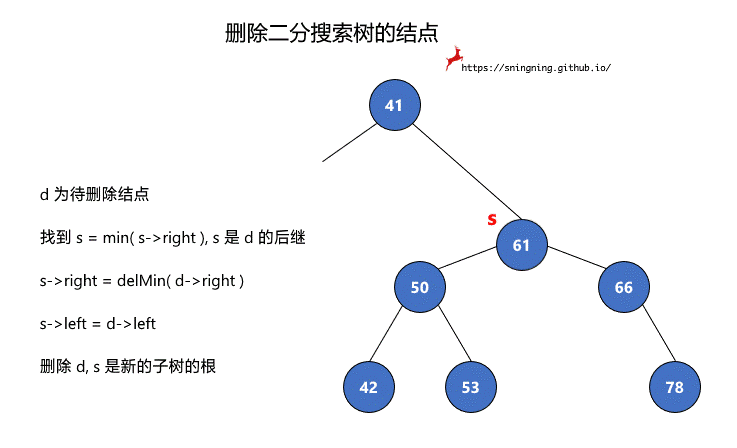
48
// 从二分搜索树中删除元素为 e 的结点
public remove(E e) {
  remove(root, e);
}

// 删除掉以 node 为根的二分搜索树中值为e的结点, 递归算法
// 返回删除结点后新的二分搜索树的根
private Node remove(Node node, E e) {

    if (node == null) {
        return null;
    }
    else if (e.compareTo(node.e) < 0) {
        node.left = remove(node.left, e);
        return node;
    }
    else if (e.compareTo(node.e) > 0) {
        node.right = remove(node.right, e);
        return node;
    }
    else {  // e.compareTo(node.e) == 0

        // 待删除结点左子树为空的情况
        if (node.left == null) {
            Node rightNode = node.right;
            node.right = null;
            size--;
            return rightNode;
        }

        // 待删除结点右子树为空的情况
        if (node.right == null) {
            Node leftNode = node.left;
            node.left = null;
            size--;
            return leftNode;
        }

        // 待删除结点左右子树均不为空的情况
        // 找到比待删除结点大的最小结点, 即待删除结点右子树的最小结点
        // 用这个结点顶替待删除结点的位置
        Node successor = minimum(node.right);
        successor.right = removeMin(node.right);
        successor.left = node.left;
        node.left = node.right = null;
        return successor;
    }
}

在最后一个 else 语句中，用了 2 个 if，而没有使用 else if，这是因为满足进入第一个 if 之后，里面直接 return 了，不会再去进行另一个 if 了，因此用 2 个 if 是没问题的。

参考资料