数组(Array),是由相同类型的元素(element)的集合所组成的数据结构,分配一块连续的内存来存储。利用元素的索引(index)可以计算出该元素对应的存储地址。维基百科
数组最大的优点就是快速查询。
1. 数组类中包含的方法
| 方法 | 描述 |
|---|---|
| Array( int capacity ) | 构造容量为 capacity 的数组类 |
| Array() | 构造默认容量的数组类 |
| int getSize() | 获取数组中元素个数 |
| int getCapacity() | 获取数组容量 |
| boolean isEmpty() | 返回数组是否为空 |
| void add( int index, E e ) | 在第 index 个位置插入一个新元素 e |
| void addLast(E e) | 向所有元素后添加一个新元素 e |
| void addFirst(E e) | 在所有元素前添加一个新元素 e |
| E get(int index) | 获取 index 索引位置的元素 |
| E getLast() | 获取最后一个元素 |
| E getFirst() | 获第一个元素 |
| void set(int index, E e)) | 修改 index 索引位置的为 e |
| boolean contains(E e) | 查询数组中是否存在元素 e |
| int find(E e) | 查询数组中元素 e 的索引位置,如果不存在,返回 -1 |
| E remove(int index) | 从数组中删除 index 位置的元素,返回被删除的元素 |
| E removeFirst() | 从数组中删除第一个元素,返回被删除的元素 |
| E removeLast() | 从数组中删除最后一个元素,返回被删除的元素 |
| void removeElement(E e) | 从数组中删除元素 e |
2. 准备工作
实现方法
| 方法 | 描述 |
|---|---|
| Array( int capacity ) | 构造容量为 capacity 的数组类 |
| Array() | 构造默认容量的数组类 |
| int getSize() | 获取数组中元素个数 |
| int getCapacity() | 获取数组容量 |
在进行数组类功能实现之前,先将基本框架搭建起来,在数组类 Array 的内部,定义一个私有数组 data 用来存放元素,定义一个 int 型私有变量 size 来表示数组元素个数。对于一些简单的方法,如获取数组元素个数、获取数组容量和判断数组是否为空,先进行实现。
1 | public class Array<E> { |
3. 添加元素
实现方法
| 方法 | 描述 |
|---|---|
| void add(int index, E e) | 在第 index 个位置插入一个新元素 e |
| void addLast(E e) | 向所有元素后添加一个新元素 e |
| void addFirst(E e) | 在所有元素前添加一个新元素 e |
| E get(int index) | 获取 index 索引位置的元素 |
| E getLast() | 获取最后一个元素 |
| E getFirst() | 获第一个元素 |
| void set(int index, E e)) | 修改 index 索引位置的为 e |
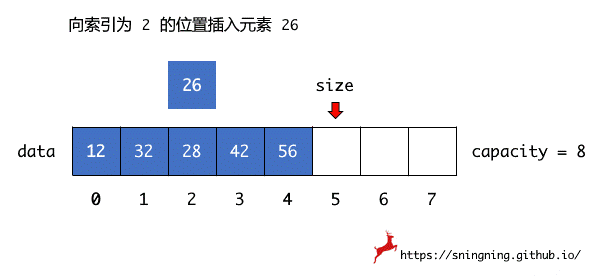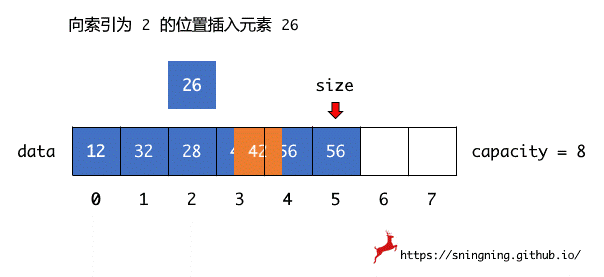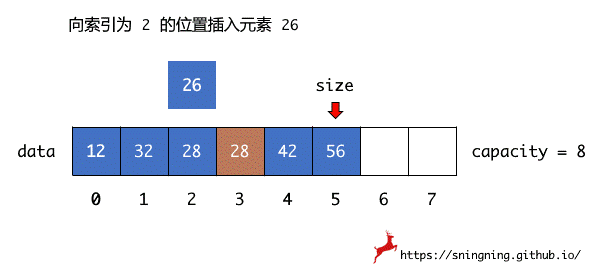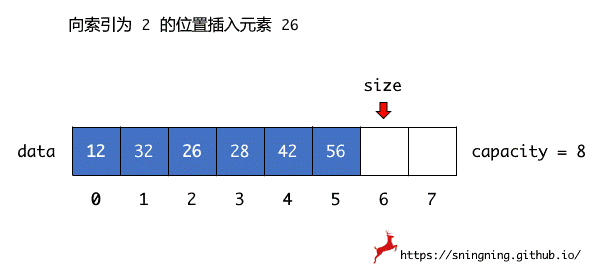
由于数组中存放元素必须是连续存储,因此在某个索引位置添加元素时,索引位置处的元素以及其后所有的元素需要依次向后移动一个位置,之后,再将元素插入指定索引位置,在后移元素时,必须是最后一个元素先进行移动。
在添加之前,还需注意两个情况:数组是否已经存满元素;传入的索引是否是合法的。对这两个情况检查完毕没有问题后,就可以将元素添加到指定索引位置,元素添加完毕后,还需要将数组元素个数加 1,即维护 size。
1 | // 在 index 索引位置插入新元素 e |
实现了在指定位置添加元素后,实现在所有元素前、在所有元素后添加元素就很简单了,只需将 add(int index, E e) 中的 index 分别设置为 0 和 size 即可。
1 | // 在所有元素后添加一个新元素 |
1 | // 在所有元素前添加一个新元素 |
4. 查询和修改元素
实现方法
| 方法 | 描述 |
|---|---|
| E get(int index) | 获取 index 索引位置的元素 |
| E getLast() | 获取最后一个元素 |
| E getFirst() | 获第一个元素 |
| void set(int index, E e)) | 修改 index 索引位置的为 e |
数组最大的优点就是可以快速查询,因此想要获取某个索引位置的元素,可以直接在数组中返回相应的元素,同样在进行查询之前,要先判断给出的 index 的合法性。
1 | // 获取 index 索引位置的元素 |
当实现了获取指定索引位置的元素后,获取最后一个和第一个元素的方法可以直接复用 get(int index)。
1 | // 获取最后一个元素 |
1 | // 获取第一个元素 |
同样,修改某个索引位置的元素同获取元素类似,只不过是将新的元素 e 赋值给数组中 index 位置即可。
1 | // 修改 index 索引位置元素为 e |
5. 包含、搜索和删除元素
实现方法
| 方法 | 描述 |
|---|---|
| boolean contains(E e) | 查询数组中是否存在元素 e |
| int find(E e) | 查询数组中元素 e 的索引位置,如果不存在,返回 -1 |
| E remove(int index) | 从数组中删除 index 位置的元素,返回被删除的元素 |
| E removeFirst() | 从数组中删除第一个元素,返回被删除的元素 |
| E removeLast() | 从数组中删除最后一个元素,返回被删除的元素 |
| void removeElement(E e) | 从数组中删除第一个元素 e |
| void removeAllElement(E e) | 从数组中删除所有元素 e |
5.1 包含、搜索元素
有时想看数组中是否包含某个元素 e,基本思路是将数组遍历,将数组元素逐一与想要查询的元素 e 进行比较,当查询到相等时,立即返回 true,否则,遍历完整个数组也没有查询到与 e 相等的元素,则返回 false。
查询数组中某个元素的索引位置,也是相同的思路,遍历数组,查询到相等时就返回当前索引位置,否则返回 -1。这里实现的 find(E e) 方法只是将该元素第一次出现的位置返回。
由于使用了泛型(Generic),因此进行元素比较时,不能使用 == 来判断,应该使用 equals() 方法。
1 | // 查询数组中是否存在元素 e |
1 | // 查询数组中元素 e 的索引位置,如果不存在,返回 -1 |
5.2 删除元素
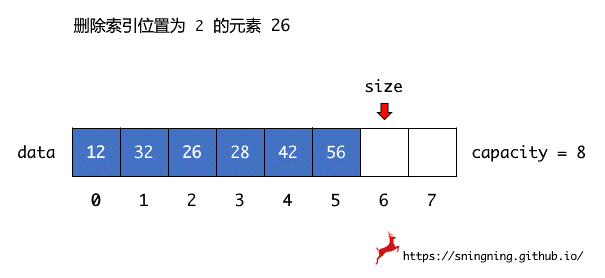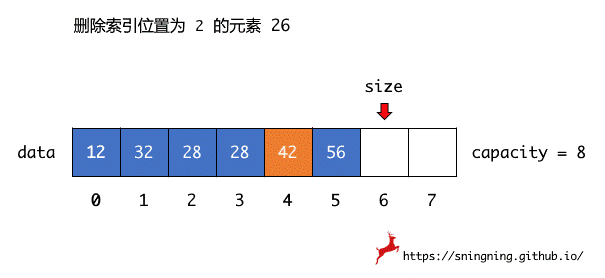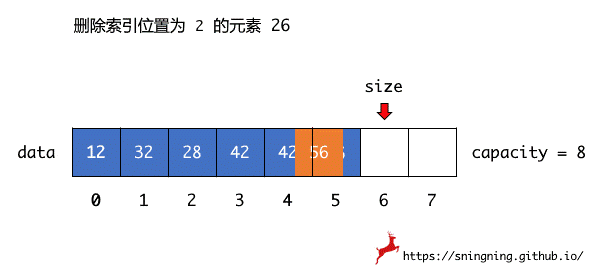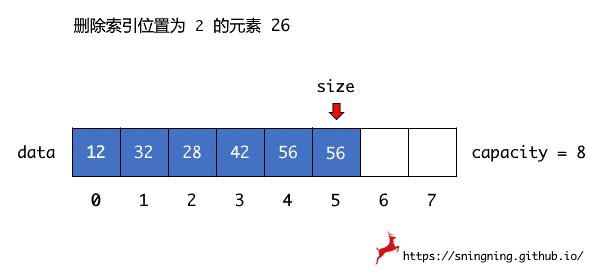
数组中的元素都是连续存储,因此删除操作实际上也是元素移动的过程,具体执行删除操作时,直接将待删除索引位置后面的元素依次向前移动覆盖,前移过程必须是待删除索引位置后第一个位置元素先进行移动。
当最后的元素 56 向前移动后,维护了 size,此时 size 指向了索引为 5 位置的 56,该元素用户是访问不到的。但是由于使用了泛型,所以实际上 size 还是指向了一个对象的引用,Java 的垃圾回收机制无法对其进行回收, 应该手动进行释放。
Java 的垃圾收集策略是回收所有无法被访问的对象的内存。在我们对 pop() 的实现中,被弹出的元素的引用仍然存在于数组中。这个元素实际上已经是一个孤儿了——它永远不会再被访问,但 Java 的垃圾收集器无法知道这一点,除非该引用被覆盖。即使用例不再需要这个元素了,数组中的引用仍然可以让它继续存在。这种情况(保存一个不需要的对象的引用)成为游离(loitering)。在这里,避免对象游离很容易,只需将被弹出的数组元素的值设为 null 即可。这将覆盖无用的引用并使系统可以在用例使用完被弹出的元素后回收它的内存。算法(第4版) P85
1 | // 从数组中删除 index 位置的元素, 返回被删除的元素 |
完成 remove(int index) 方法后,删除数组中第一个元素和最后一个元素,直接复用 remove(int index) 方法,传入相应的索引即可。
1 | // 从数组中删除第一个元素, 返回被删除的元素 |
1 | // 从数组中删除最后一个元素, 返回被删除的元素 |
要实现从数组中删除某一个元素 e,可以先调用 find(E e) 方法,找到其在数组中对应的索引位置,然后再调用 remove(int index) 方法,将其删除。如果调用 find(E e) 返回 -1,即数组中不存在该元素,这里不执行任何操作。实现的 removeElement(E e) 方法,由于只进行了一次 find 操作,因此只能删除第一次出现的 e。
1 | // 从数组中(第一次出现 e 的位置)删除元素 e |
6. 动态调整容量
前面所有操作的实现,底层都是基于 data 数组,当实例化 Array 类后,底层 data 数组的容量就已经固定了。如果不断向数组中添加元素,势必会导致数组被填满,因此可以考虑,在添加完元素后,当满足一定条件时,进行底层 data 数组的扩容;另一方面,当删除完元素后,可以考虑当满足一定条件时,对底层 data 数组进行缩容。
数组大小的动态调整(缩容或扩容),实质上是将原来数组的元素,逐个复制到新的数组中,然后将之前的数组引用 data 指向新的数组,Java 的垃圾回收机制会将之前的数组进行回收。这里实现一个私有的方法 resize(int newCapacity) 来调整数组容量,设置成私有方法是因为,对于使用 Array 类的用户来说,容量调整这个过程是对其屏蔽的。
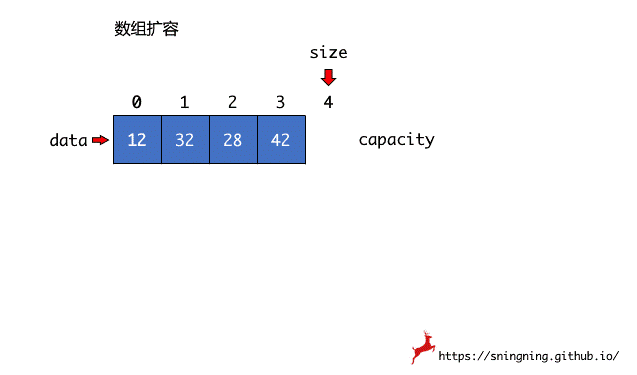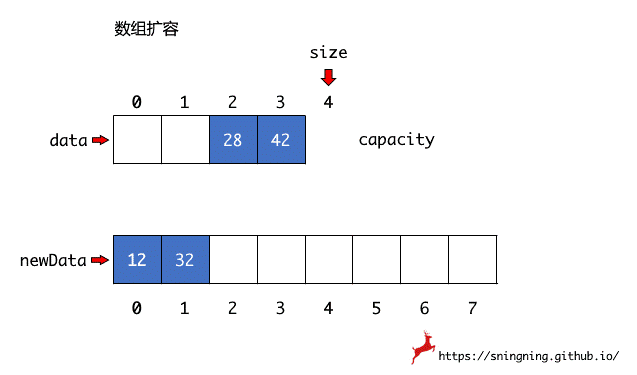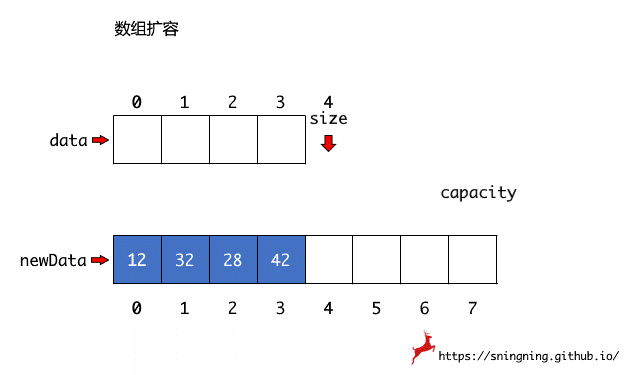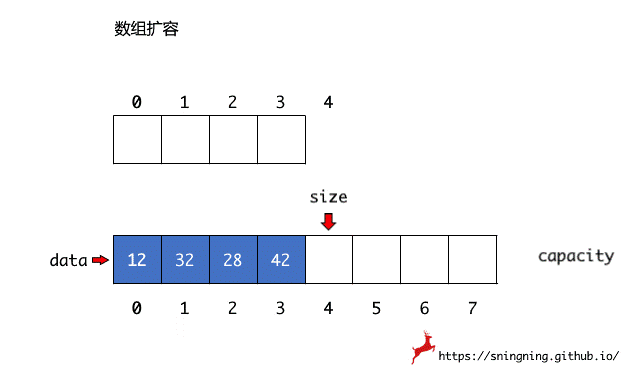
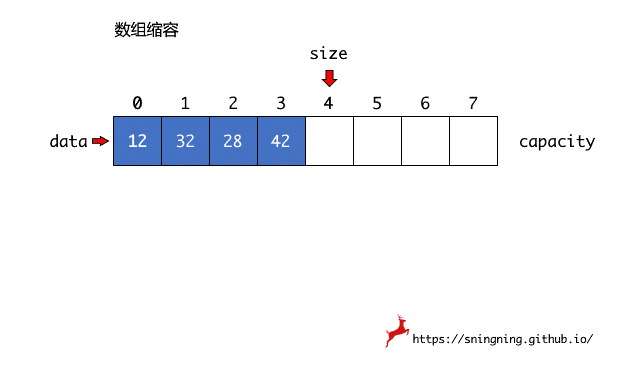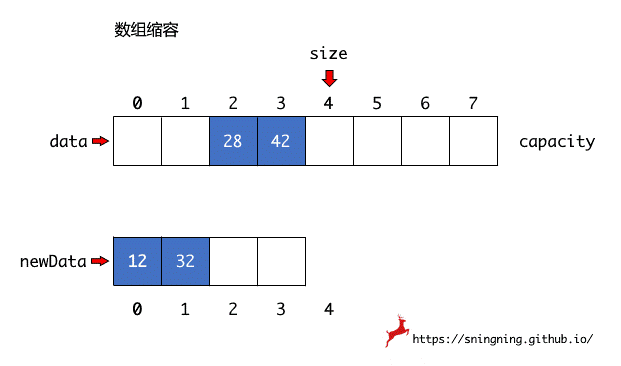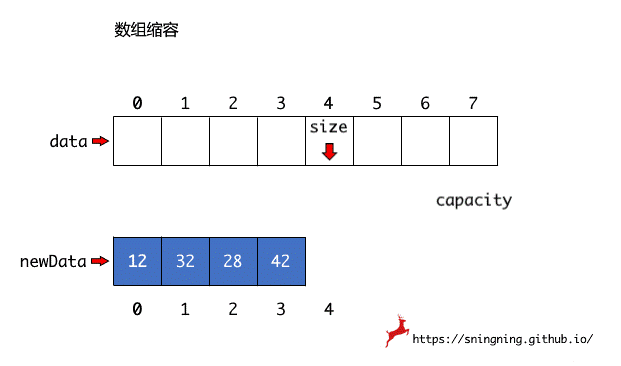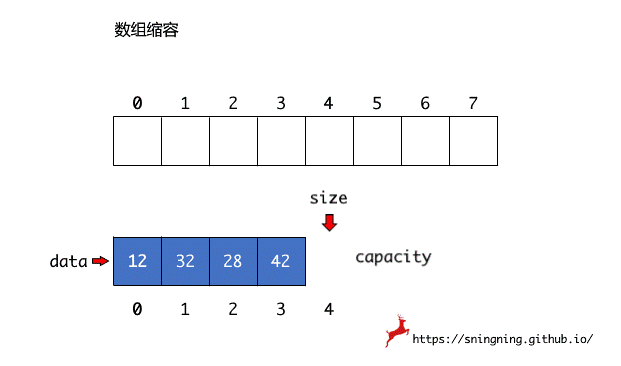
1 | // 数组容量调整 |
6.1 扩容
扩容,是在添加元素时进行的,前面实现的 add(int index, int e) 方法中,对于数组已满的情况是抛出了异常,现在可以将底层 data 数组进行扩容,扩容的大小设置为当前容量的 2 倍,即 2 * data.length,这里设置的新数组的容量是与现有元素个数相关联的,保证新数组容量和之前数组中元素的个数是一个数量级。
在 Java 中,ArrayList 扩容是变为原来的 1.5 倍。在 ArrayList 类的 grow(int minCapacity) 私有方法中, int newCapacity = oldCapacity + (oldCapacity >> 1); 进行了新容量的设定。
1 | // 在第 index 个位置插入一个新元素 e |
6.2 缩容
在删除对象后,可以根据元素个数进行缩容操作。当元素个数小到刚好等于数组长度的一半时,即 size == data.length / 2,将数组缩容为原来长度的一半。暂时这样处理,后续再进行优化。
1 | // 从数组中删除 index 位置的元素, 返回删除的元素 |
7. 简单的时间复杂度分析
7.1 添加操作的时间复杂度
| 添加操作 | 时间复杂度 |
|---|---|
| addLast(E e) | O(1) |
| addFirst(E e) | O(n) |
| add(int index, E e) | O(n/2) = O(n) |
有时添加元素时还需要扩容,resize 操作的时间复杂度为 O(n),因此,总体来看,添加操作的时间复杂度为 O(n)。
7.2 删除操作的时间复杂度
| 删除操作 | 时间复杂度 |
|---|---|
| removeLast(E e) | O(1) |
| removeFirst(E e) | O(n) |
| remove(int index, E e) | O(n/2) = O(n) |
有时删除元素后还需要缩容,resize 操作的时间复杂度为 O(n),因此,总体来看,删除操作的时间复杂度为 O(n)。
7.3 修改、查询操作的时间复杂度
| 操作 | 时间复杂度 |
|---|---|
| set(int index, E e) | O(1) |
| get(int index) | O(1) |
| contains(E e) | O(n) |
| find(E e) | O(n) |
8. 改进缩容操作
假设当前数组容量为 8,即 capacity = 8。添加 9 个元素,每次添加操作均使用 addLast() ,则一共需要 9 次 addLast() 操作和 1 次 resize(2 * 8) 操作。其中, resize(2 * 8) 需要将已有的 8 个元素全部进行复制,因此总共进行了 17 次基本操作。平均来看,每次 addLast() 操作会进行 2 次基本操作。
更普遍的,假设 capacity = n,n + 1 次 addLast() ,触发 resize 操作,总共进行了 n + n + 1 = 2n + 1 次基本操作。平均来看,每次 addLast() 操作会进行 2 次基本操作。这里 1 次 resize 的时间平摊给了 n + 1 次 addLast() 操作,这样均摊来看,addLast() 的时间复杂度为 O(1),因此在这里 addLast() 的均摊复杂度(Amortized Time Complexity) 为 O(1)。
同理,从均摊复杂度分析,removeLast() 的摊复杂度也是 O(1)。
但是,当 size == data.length,也就是 size == capacity 时,依次进行 addLast() 和 removeLast() 操作,根据之前 add 和 remove 中扩容缩容的条件,会出现复杂度振荡的情况。

出现复杂度振荡的原因,是在进行 removeLast() 操作时 resize 过于着急(eager) ,当元素个数等于数组容量的一半时马上进行缩容,缩容完整个 data 数组是满的,再添加元素肯定需要再进行扩容。解决的方法就是采用 懒惰 (lazy) 的方案,当 size == data.length / 4 时,再进行容量减半,此时缩容完,data 数组还有一半的空余容量。
注意,因为是要缩容,data.length 要减小,有可能 data.length == 1,此时 data.length / 2 == 0,因此缩容前应该进行判断。
1 | // 从数组中删除 index 位置的元素,返回被删除的元素 |

9. 数组类的整体实现
为了方便打印输出,重写了 toString() 方法。整体实现:Array.java
1 |
|

