数据结构02-栈和队列

栈（Stack）是一种后入先出（Last In First Out, LIFO）的线性数据结构， 只能从一端添加或取出元素，进出元素的一端称为栈顶。
队列（Queue）是一种先入先出（First In First Out, FIFO）的线性数据结构，只能从一端添加元素，从另一端取出元素，添加元素一端称为队尾，取出元素的一端称为队首。

1.栈（Stack）

1.1 栈的接口中定义的几个操作

方法	描述
int getSize()	获取栈中元素个数
boolean isEmpty()	判断栈是否为空
void push(E e)	入栈，向栈中压入元素 e
E pop()	出栈，弹出栈顶元素
E peek()	查看栈顶元素

public interface Stack<E> {

    // 获取栈中元素个数
    int getSize();

    // 判断栈是否为空
    boolean isEmpty();

    // 入栈，向栈中压入元素 e
    void push(E e);

    // 出栈，弹出栈顶元素
    E pop();

    // 查看栈顶元素
    E peek();
}

1.2 基于 Array 类的栈实现

如果用之前实现的动态数组 Array 类来实现栈，很多方法可以直接复用。由于在数组的末尾添加元素和删除元素的复杂度为 O(1)，因此将数组的末尾作为栈顶。

在实现栈中 push(E e) 和 pop() 方法时，根据后入先出的原则，分别复用 Array 中的 addLast(E e) 和 removeLast() 方法。peek() 操作只是查看栈顶元素，并非删除，因此复用 Array 类中的 getLast() 方法。

另外再添加 getCapacity() 方法，返回当前栈的容量，具体实现是返回底层数组的容量。

public class ArrayStack<E> implements Stack<E> {

    private Array<E> array;

    public ArrayStack(int capacity) {
        this.array = new Array<>(capacity);
    }

    public ArrayStack() {
        this.array = new Array<>();
    }

    public int getCapacity(){
        return array.getCapacity();
    }

    @Override
    public int getSize() {
        return array.getSize();
    }

    @Override
    public boolean isEmpty() {
        return array.isEmpty();
    }

    @Override
    public void push(E e) {
        array.addLast(e);
    }

    @Override
    public E pop() {
        return array.removeLast();
    }

    @Override
    public E peek() {
        return array.getLast();
    }
}

为了方便打印输出，重写一下 toString() 方法。数组栈的整体实现：ArrayStack.java

@Override
public String toString() {

    StringBuilder res = new StringBuilder();
    res.append("Stack: ");
    res.append('[');
    for (int i = 0 ; i < array.getSize() ; i ++) {

            res.append(array.get(i));
            if (i != array.getSize() - 1) {
                res.append(", ");
            }
    }
    res.append("] top");

    return res.toString();
}

1.3 栈的复杂度分析

由于 push(E e) 和 pop() 操作都是在数组尾操作，因此时间复杂度是 O(1)，如果触发 resize() 操作，按照均摊复杂度分析，整个过程也是 O(1)。

方法	复杂度
int getSize()	O(1)
boolean isEmpty()	O(1)
void push(E e)	O(1) 均摊
E pop()	O(1) 均摊
E peek()	O(1)

---

2. 队列（Queue）

2.1 队列的接口中定义的几个操作

方法	描述
void enqueue(E e)	入队，向队列中添加新元素 e
E dequeue()	出队，从队列中删除元素
E getFront()	查看队首元素
int getSize()	获取队列中元素个数
boolean isEmpty()	判断队列是否为空

public interface Queue<E> {

    // 入队，向队列中添加新元素 e
    void enqueue(E e);

    // 出队，从队列中删除元素
    E dequeue();

    // 查看队首元素
    E getFront();

    // 获取队列中元素个数
    int getSize();

    // 判断队列是否为空
    boolean isEmpty();
}

2.2 基于 Array 类的队列实现

还是用之前实现的动态数组 Array 类来实现队列，很多方法可以直接复用。

在实现队列中 enqueue(E e) 和 dequeue() 方法时，根据先入先出的原则，分别复用 Array 中的 addLast(E e) 和 removeFirst() 方法。getFront() 操作只是查看队首元素，并非删除，因此复用 Array 类中的 getFirst() 方法。

另外再添加 getCapacity() 方法，返回当前栈的容量，具体实现是返回底层数组的容量。

public class ArrayQueue<E> implements Queue<E> {

    private Array<E> array;

    public ArrayQueue(int capacity){
        this.array = new Array<>(capacity);
    }

    public ArrayQueue() {
        this.array = new Array<>();
    }

    public int getCapacity(){
        return array.getCapacity();
    }

    @Override
    public void enqueue(E e) {
        array.addLast(e);
    }

    @Override
    public E dequeue() {
        return array.removeFirst();
    }

    @Override
    public E getFront() {
        return array.getFirst();
    }

    @Override
    public int getSize() {
        return array.getSize();
    }

    @Override
    public boolean isEmpty() {
        return array.isEmpty();
    }
}

为了方便打印输出，重写 toString() 方法。数组队列的整体实现：ArrayQueue.java。

@Override
public String toString() {
    
    StringBuilder res = new StringBuilder();
    res.append("Queue: ");
    res.append("front [");
    for(int i = 0 ; i < array.getSize() ; i ++) {
        
        res.append(array.get(i));
        if(i != array.getSize() - 1) {
            res.append(", ");
        }
    }
    res.append("] tail");

    return res.toString();
}

2.3 队列的复杂度分析

由于 enqueue(E e) 操作是在数组尾操作，因此时间复杂度是 O(1)，如果触发 resize() 操作，按照均摊复杂度分析，入队过程也是 O(1)。

但出队操作是在数组头部进行，底层复用动态数组类中 removeFirst() 方法，因此时间复杂度为 O(n)。

方法	复杂度
void enqueue(E e)	O(1) 均摊
E dequeue()	O(n)
E getFront()	O(1)
int getSize()	O(1)
boolean isEmpty()	O(1)

---

3. 循环队列

3.1 循环队列介绍

之前用动态数组实现的队列，出队操作由于复用了动态数组中 removeFirst() 操作，删除第一个元素后，后面的元素需要向前依次移动，因此时间复杂度为 O(n)。

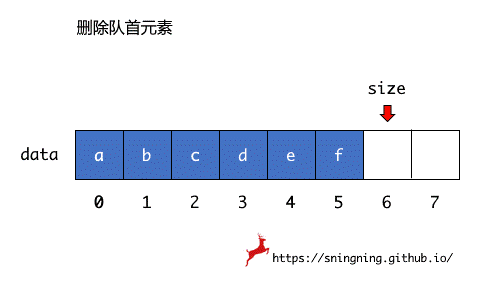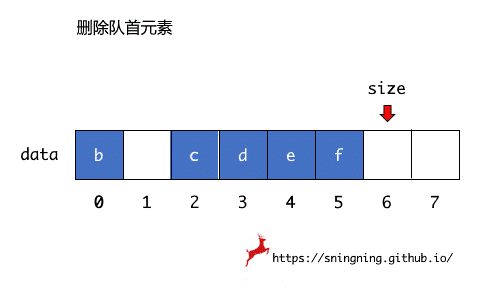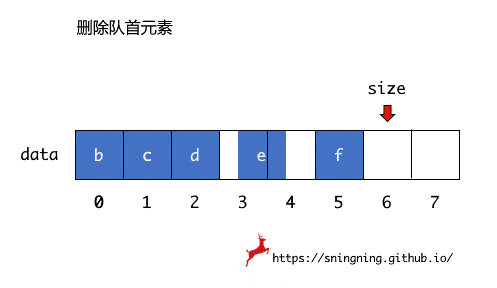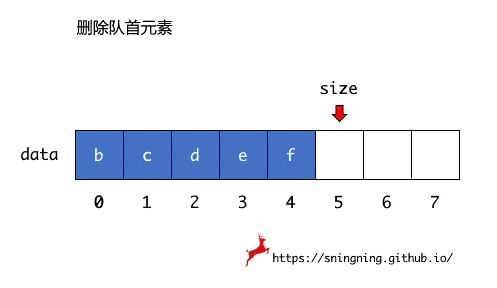
考虑出队后，其余元素不进行移动，这样就可以使出队的时间复杂度变为 O(1)。

当删除数组第一个元素后，不进行后面元素的移动，而是用一个 front 变量记录下当前第一个元素的索引位置，即队首元素位置，同时用一个 tail 变量记录下最后一个元素的下一个索引位置，也是新元素入队时的索引位置。这样当删除数组第一个元素后，只需要维护 front 就可以。

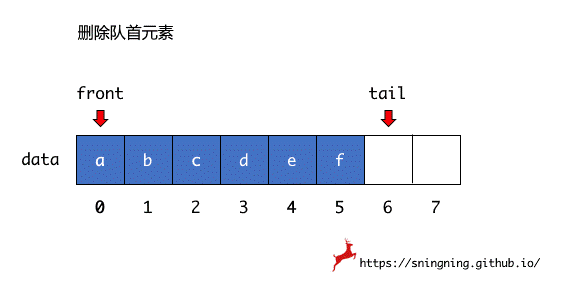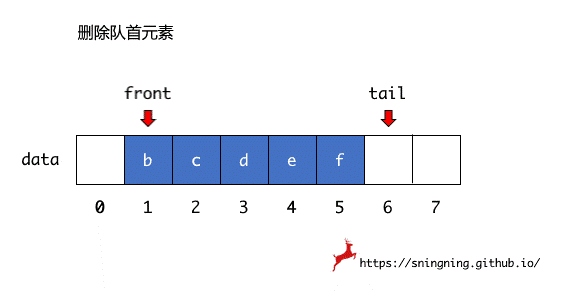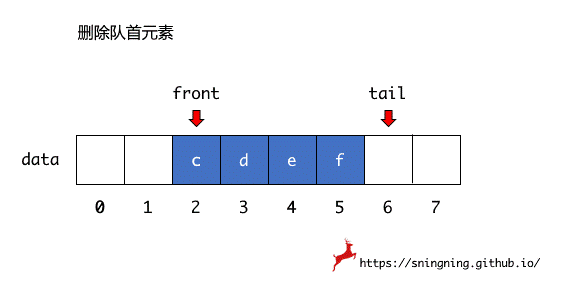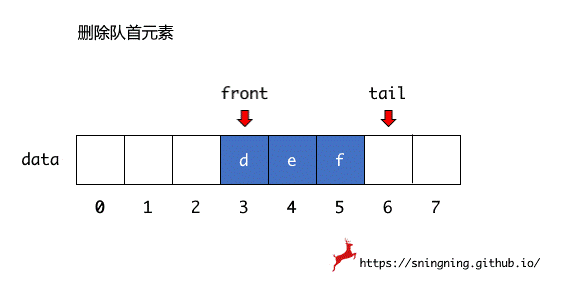
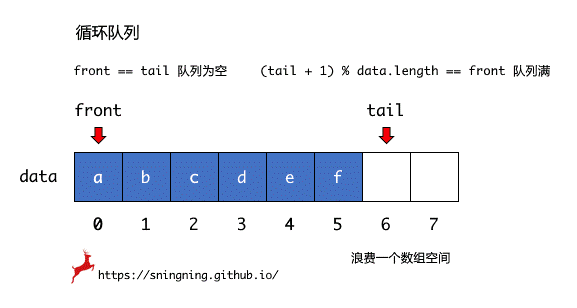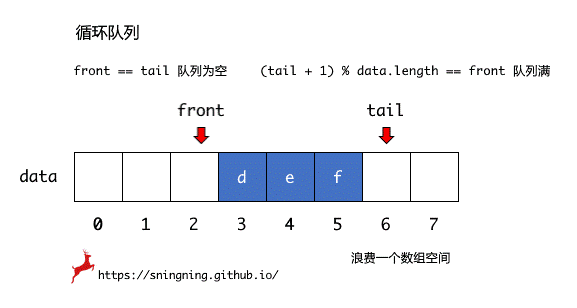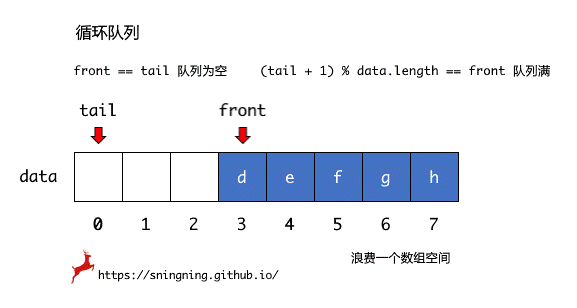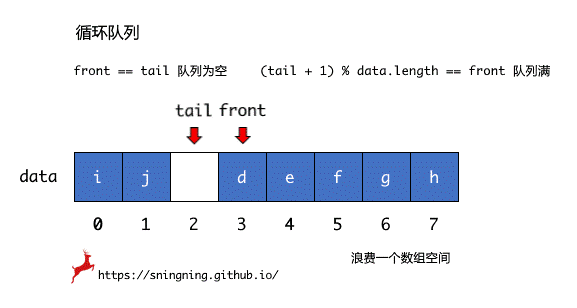
循环队列的初始状态下，队列中没有元素，front 和 tail 均指向底层数组的第一个位置，因此当 front == tail 时，队列为空。

进行入队操作时，只需维护 tail；如果进行出队操作，只需维护 front。

当底层数组中最后一个位置存在元素，再进行入队操作时，tail 就无法进行简单的 tail++ 操作，但是由于进行了出队操作，底层数组的前半部分是空闲的，如下图中所示，这时 tail 应该指向 data[0]，因此要实现这种循环的操作，tail 的维护应该变成 tail = (tail + 1) % data.length。

当底层数组中 tail + 1 == front时，再添加元素，此时 front == tail，而前面定义这种情况是队列为空的判断条件，因此在这种情况下，选择不再添加元素，即判断队列为满的条件是 tail + 1 == front，但由于是循环队列，这个判断条件响应改为 (tail + 1) % data.length == front，如同钟表一样，11 点的下一个小时我们可以说是 12 点或者是 0 点，钟表中的 12 个刻度对应底层数组的长度 data.length。这时浪费了一个数组空间，因此当前队列所能存储最多的元素个数为 data.length - 1。

3.2 循环队列中简单方法的实现

先进行 LoopQueue 类中简单操作的实现，由于实现方式不同，这里不再复用之前的 Array 动态数组类。

public class LoopQueue<E> implements Queue<E> {

    private E[] data;
    private int front, tail;
    private int size;   

    public LoopQueue(int capacity) {
      
        data = (E[])new Object[capacity + 1];
        front = 0;  // 队列中第一个元素的索引
        tail = 0;   // 队列中最后一个元素的下一个索引
        size = 0;   // 队列中元素个数
    }

    public LoopQueue() {
        this(10);
    }

    public int getCapacity() {
        return data.length - 1;
    }

    @Override
    public boolean isEmpty() {
        return front == tail;
    }

    @Override
    public int getSize() {
        return size;
    }

    // 后面实现
    @Override
    public void enqueue(E e) {

    }

    // 后面实现
    @Override
    public E dequeue() {
        return null;
    }

    // 后面实现
    @Override
    public E getFront() {
        return null;
    }
}

3.3 底层数组容量调整

底层数组的容量调整和之前 Array 中 resize(int newCapacity) 方法类似。差别在于两个地方：遍历旧数组、维护 front 和 tail。

为了保证元素的顺序，必须从 front 开始遍历旧的 data 数组时，但旧数组中 front 可能不为 0，即不能进行 newData[i] = data[i] 这种操作，这时 data 中元素相对于 newData 中元素的索引值存在 front 数量的偏移，同时由于是循环队列，有可能会产生越界，需要再对 data.length 进行取模。这里也有两种遍历方式。

方式一：终止条件从 size 考虑。

for (int i = 0; i < size; i++) {
    newData[i] = data[(i + front) % data.length];
}

方式二：终止条件从 tail 考虑。

for (int i = front ; i != tail ; i = (i + 1) % data.length) {
    newData[(i - front) % data.length] = data[i];
}

在容量调整后，front 重新指向了新数组索引为 0 的位置，tail 重新指向了新数组中索引为 size 的位置。

private void resize(int newCapacity) {

    E[] newData = (E[]) new Object[newCapacity + 1];

    for (int i = 0; i < size; i++) {
        newData[i] = data[(i + front) % data.length];
    }

    data = newData;
    front = 0;
    tail = size;
}

3.4 循环队列入队、出队的实现

循环队列底层数组的添加、删除和容量调整的方式和 Array 中的方法基本是相同的，差别主要在于维护 front 和 tail 变量时并不是简单加一，而是需要加一并取模数组长度。

@Override
public void enqueue(E e) {

    if ( (tail + 1) % data.length == front ) {
        resize( getCapacity() * 2 );
    }

    data[tail] = e;
    tail = (tail + 1) % data.length;
    size++;
}

@Override
public E dequeue() {

    if (isEmpty()) {
        throw new IllegalArgumentException("出队失败，队列为空。");
    }

    E ret = data[front];
    data[front] = null;
    front = (front + 1) % data.length;
    size--;

    if (size == getCapacity() / 4 && getCapacity() / 2 != 0) {
        resize(getCapacity() / 2);
    }

    return ret;
}

重写 toString() 方法，循环队列的整体实现：LoopQueue.java

@Override
public String toString() {

    StringBuilder res = new StringBuilder();
    res.append(String.format("Queue: size = %d , capacity = %d\n", size, getCapacity()));
    res.append("front [");
    
    for (int i = front ; i != tail ; i = (i + 1) % data.length) {

        res.append(data[i]);
        if ((i + 1) % data.length != tail) {
            res.append(", ");
        }
    }
    res.append("] tail");

    return res.toString();
}

3.5 循环队列的时间复杂度

方法	复杂度
void enqueue(E e)	O(1) 均摊
E dequeue()	O(1) 均摊
E getFront()	O(1)
int getSize()	O(1)
boolean isEmpty()	O(1)

---

参考资料

• 玩转数据结构
• VisuAlgo
• 算法(第4版)
• Algorithms(4th edition)